K. 96. The sides of an equilateral triangle ABC are 16 cm long. The side AC is extended beyond A by one quarter of the length AC and the point P is obtained. The point P is connected by a line to the point dividing the side AB in a 1:3 ratio (so that the shorter segment of AB lies next to A.) This line divides the side BC into two pieces. Find their lengths.

(6 points)

Deadline expired.

Sorry, the solution is published in Hungarian only.

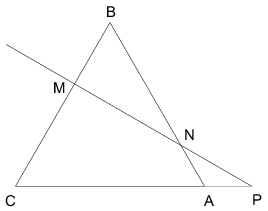
Megoldás. Legyen az AB oldal A-hoz közelebbi negyedelőpontja N, PN és BC metszéspontja M. Ekkor a PAN háromszög egyenlő szárú, melynek alapon fekvő szögei 30 fokosak. Emiatt a BNM háromszög szögei 30, 60, 90 fokosak. Mivel BN=12 cm, ezért BM=6 cm és MC=10 cm.

Statistics on problem K. 96. 244 students sent a solution. 6 points: 122 students. 5 points: 19 students. 4 points: 17 students. 3 points: 13 students. 2 points: 8 students. 1 point: 1 student. 0 point: 62 students. Unfair, not evaluated: 2 solutions.