 Problem P. 4107. (November 2008)
Problem P. 4107. (November 2008)
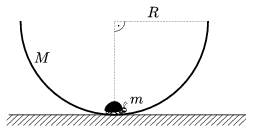
P. 4107. A small beetle of mass m is slowly crawling out from the bottom of a hemi-sphere shaped shell. The mass of the shell is M and its radius is R. How much work does the beetle perform until it reaches the rim of the hemi-sphere? (The coefficient of static friction between the beetle and the shell is large enough.)
(4 pont)
Deadline expired on December 11, 2008.
Statistics:
67 students sent a solution. 4 points: Balassa Péter, Barancsuk Lilla, Boros Csanád Örs, Csengeri Béla, Fonai Dániel, Földes Imre, Galzó Ákos Ferenc, Garaguly Gergő, Harnos Balázs, Hartstein Máté, Illés Dorottya, Ji Hai Ou, Kaposvári István, Lászlóffy András, Marák Károly, Márkus Bence Gábor, Mayer Martin János, Molnár Gabriella, Mozsáry László, Nagy 127 Márton, Pálovics Péter, Paripás Viktor, Schwarcz Gergő, Somogyi József, Szédelyi Roland, Tamási Mátyás, Timár Máté, Tóth 222 Barnabás, Török Lajos, Wang Daqian, Zsolczai Viktor. 3 points: Tószegi Károly. 2 points: 5 students. 1 point: 10 students. 0 point: 16 students. Unfair, not evaluated: 4 solutionss.
Problems in Physics of KöMaL, November 2008
