 Problem P. 4237. (March 2010)
Problem P. 4237. (March 2010)
P. 4237. A path is made to a uniform density cube of mass m, and of edge a, such that when the cube rolls along the path without skiding, its centre moves along a straight line (``square wheel''). At the ``top'' of the path a horizontal initial velocity of v0 is given to the centre of the cube. The static frictional force is big enough, so the cube do not slide anywhere. What is the speed of the centre of mass when the cube touches the lowest point of the path? (The moment of inertia of the cube with respect to its centre of mass is )
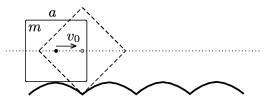
(4 pont)
Deadline expired on April 12, 2010.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. \(\displaystyle \sqrt{5}v_0/2\approx1,\!12v_0.\)
Statistics:
45 students sent a solution. 4 points: Béres Bertold, Bolgár Dániel, Börcsök Bence, Fekete Károly, Galzó Ákos Ferenc, Jéhn Zoltán, Kánvási Dániel, Kaposvári István, Koncz Gabriella, Kószó Simon, Kungl Ákos Ferenc, Kunsági-Máté Sándor, Láng Hanga, Németh Gábor , Neumer Tamás, Pálovics Péter, Patartics Bálint, Petrács Ervin, Szabó 928 Attila, Szécsényi 136 Andrea, Szélig Áron, Szentgyörgyi 994 Rita, Timkó Réka, Virág Máté. 3 points: Balogh Gábor, Czigány Máté Gábor, Pázmán Koppány. 2 points: 3 students. 1 point: 9 students. 0 point: 6 students.
Problems in Physics of KöMaL, March 2010
