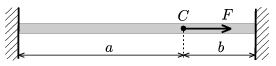
P. 4256. A rubber cord is stretched out between two walls. At the point of the cord C a force of F along the direction of the cord is exerted.

a) What is the displacement of point C if the cord can be characterized with a spring constant D?

b) At which point of the cord must the force F be exerted when the displacement of C is the greatest?

Data: F=5 N, a=40 cm, b=10 cm, .

(4 points)

Deadline expired.

Sorry, the solution is published in Hungarian only.

a)

b) Az ab/(a+b)² arányt kell maximalizálnunk az a+b=állandó mellékfeltétel mellett. Ez ekvivalens azzal a problémával, hogy adott kerületű téglalapok közül melyiknek legnagyobb a területe, melyre a válasz a négyzet. Tehát az a=b feltételnek eleget tevő középső pontban kell erővel hatni a gumiszálra, hogy a megragadott pont elmozdulása a lehető legnagyobb legyen. (Ez a megoldás csak akkor érvényes, ha a gumiszál mindvégig feszes marad, nem lazul meg.)

Statistics on problem P. 4256. 59 students sent a solution. 4 points: Batki Bálint, Borszuk Adrienn, Czigány Máté Gábor, Farkas Martin, Hegedűs Csaba, Horicsányi Attila, Kovács 255 Márton, Laczkó Zoltán Balázs, Láng Hanga, Neumer Tamás, Pál Domonkos, Patartics Bálint, Sisák Mária Anna, Szigeti Bertalan György, Szikszai Lőrinc, Tamási Mátyás, Varju 105 Tamás, Vuchetich Bálint, Zsiros Ádám. 2 points: 28 students. 1 point: 6 students. 0 point: 6 students.