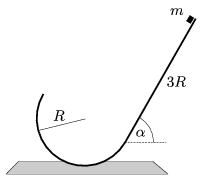
P. 4308. The bottom end of a smooth inclined plane of angle of elevation =60^o, and of length 3R is attached to a cylinder, which has a semicircular cross section of radius R=0.5 m. In the path there is no break. From the top of the inclined plane a pointlike object of mass m=0.2 kg slides down with zero initial speed. a) What will the kinetic energy of the object be at the highest point of the curved part of the path? b) Where will the object hit the inclined plane? (Friction and air drag are negligible.)

(5 points)

Deadline expired.

Sorry, the solution is published in Hungarian only.

a) A kis test mechanikai energiája megmarad, ezért pályájának legmagasabb pontján a mozgási energiája

értékű lesz.

b) A kis test a lejtő és a hengerfelület csatlakozási vonalától

távolságra csapódik a lejtőbe (ennek kiszámítására a legegyszerűbb mód, ha elforgatott koordinátarendszert használunk).

Statistics on problem P. 4308. 110 students sent a solution. 5 points: Ayhan Dániel, Barta Szilveszter Marcell, Batki Bálint, Bolgár Dániel, Csáky Pál, Fonyó Viktória, Garami Anna, Jenei Márk, Kabos Eszter, Kovács 255 Márton, Maknics András, Nagy Lajos, Papp Roland, Pataki Bálint Ármin, Sisák Mária Anna, Szabó 928 Attila, Szegedi Domonkos, Szélig Áron, Szikszai Lőrinc, Tamási Mátyás, Varga 515 Balázs, Zsámboki Richárd. 4 points: Antalicz Balázs, Béres Bertold, Csóka József, Dálya Gergely, Damokos József, Emri Tamás, Gargauly Gergő János, Gróf Gábor, Kalácska Dániel, Kaposvári Péter, Károlyi Áron, Kollarics Sándor, Koncz Gabriella, Kovács 737 Ármin, Kozák Ádám András, Kunsági-Máté Sándor, Lőrincz Dóra, Nagy Dániel Bálint, Németh 241 Ilona, Park Choong Eun, Schwarcz Gergő, Simon Sebestyén, Szigeti Bertalan György, Timkó Réka, Zahemszky Péter. 3 points: 31 students. 2 points: 12 students. 1 point: 7 students. 0 point: 5 students. Unfair, not evaluated: 8 solutions.