Problem P. 4324. (February 2011)

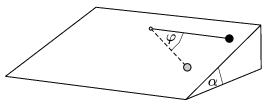
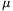P. 4324. One end of a thread of length l=1 m is attached to an inclined plane of angle of elevation of $\alpha$ =30^o. A point-like body of mass m=1 kg is attached to the other end of the thread as shown in the figure. The body is released without initial speed, such that the thread is tight and horizontal. The coefficient of friction between the slope and the body is $\mu$ =0.2. a) Determine the maximum speed of the sliding body. b) Find the tension in the thread when the angle between the thread and the horizontal is first 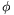$\phi$ =60^o. c) In which position of the thread will the tension be maximum?

(5 pont)

Deadline expired on March 10, 2011.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. $\displaystyle a$) Ha a test sebessége maximális, akkor az érintőleges gyorsulása épp zérus:

$\displaystyle mg \sin \alpha \cos \varphi-\mu mg \cos \alpha =0,$

ebből a maximális sebességnek megfelelő helyzet: $\displaystyle \varphi=\arccos \left( \frac{\mu}{tg \alpha}\right)\approx 69,\! 7^{\circ}$.

$\displaystyle b)$ A munkatételből és a Newton-féle mozgásegyenlet sugárirányú komponenséből a fonálerő nagysága egy $\displaystyle \varphi$ szögű helyzetben:

$\displaystyle F=(3\sin \varphi \sin \alpha -2\mu \varphi \cos\alpha)mg,$

így pl. $\displaystyle \varphi=60^{\circ}$-ra $\displaystyle F\approx 9,\! 2$ N.

$\displaystyle c$) Az $\displaystyle F$ erő fenti kifejezéséből deriválással vagy elemi megfontolásokkal megkapható a fonálerő maximumának helye: $\displaystyle \varphi=\arccos\left( \frac{2\mu}{3 \tg \alpha}\right)\approx 76,\!6 ^{\circ}.$

Statistics:

69 students sent a solution.

5 points: Ábrahám Attila, Antalicz Balázs, Barta Szilveszter Marcell, Batki Bálint, Béres Bertold, Bojtár Orsika, Filep Gábor, Horváth 721 Klaudia, Jéhn Zoltán, Jenei Márk, Juhász Péter, Koncz Gabriella, Kovács 444 Áron, Kunsági-Máté Sándor, Laczkó Zoltán Balázs, Mázik László, Nagy 111 Miklós, Papp Roland, Park Choong Eun, Pázmán Koppány, Szabó 928 Attila, Tamási Mátyás, Ürge László, Várnai Péter, Zahemszky Péter.

4 points: Bolgár Dániel, Herczeg Ferenc, Kollarics Sándor, Maknics András, Pataki Bálint Ármin, Szélig Áron, Szentgyörgyi 994 Rita, Tóth Balázs.

3 points: 9 students.

2 points: 6 students.

1 point: 14 students.

0 point: 4 students.

Unfair, not evaluated: 3 solutionss.

Problems in Physics of KöMaL, February 2011

69 students sent a solution.
5 points:	Ábrahám Attila, Antalicz Balázs, Barta Szilveszter Marcell, Batki Bálint, Béres Bertold, Bojtár Orsika, Filep Gábor, Horváth 721 Klaudia, Jéhn Zoltán, Jenei Márk, Juhász Péter, Koncz Gabriella, Kovács 444 Áron, Kunsági-Máté Sándor, Laczkó Zoltán Balázs, Mázik László, Nagy 111 Miklós, Papp Roland, Park Choong Eun, Pázmán Koppány, Szabó 928 Attila, Tamási Mátyás, Ürge László, Várnai Péter, Zahemszky Péter.
4 points:	Bolgár Dániel, Herczeg Ferenc, Kollarics Sándor, Maknics András, Pataki Bálint Ármin, Szélig Áron, Szentgyörgyi 994 Rita, Tóth Balázs.
3 points:	9 students.
2 points:	6 students.
1 point:	14 students.
0 point:	4 students.
Unfair, not evaluated:	3 solutionss.

Already signed up?
New to KöMaL?