Problem P. 4330.

Order KöMaL!

ELTE

Competitions Portal

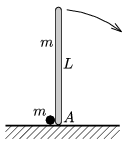
P. 4330. A thin, L=2 m long rod of mass m is standing vertically on a horizontal frictionless plane. Next to its bottom endpoint A there is a pointlike object of mass m at rest. The rod fells out of its unstable equilibrium position, such that the paths of the small body and the rod are always in the same plane. What is the greatest speed of the small body?

(6 points)

Deadline expired.

Sorry, the solution is published in Hungarian only.

Ha a pálca $\theta$ szöget zár be a függőlegessel, a kis test sebessége

$v=\sqrt{gL\frac{\cos^2\theta-\cos^3\theta}{\frac{16}3-2\cos^2\theta}}\le 0{,}82~\frac{\rm m}{\rm s}.$

Statistics on problem P. 4330.

28 students sent a solution.

6 points: Béres Bertold, Kovács 444 Áron, Laczkó Zoltán Balázs, Nagy Lajos, Papp Roland, Szabó 928 Attila, Szigeti Bertalan György, Várnai Péter, Ürge László.

5 points: Bolgár Dániel, Nagy Dániel Bálint, Sárvári Péter, Szélig Áron.

4 points: 2 students.

3 points: 4 students.

2 points: 4 students.

1 point: 3 students.

0 point: 2 students.

Problems in Physics of KöMaL, March 2011

Our web pages are supported by:

ELTE