Problem P. 4496. (December 2012)

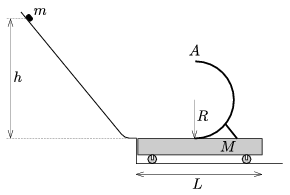
P. 4496. A small object of mass m slides along a slope which is attached tangentially to a cart of mass M. In the middle of the cart a hemicylinder of radius R is attached to the cart as shown in the figure. The small object of mass m just reaches the top point A of this hemicylinder, stops there for an instant, then it falls freely and just hits the rim of the car. a) At least how long is the cart? b) What is the mass of the cart? c) From what height did the small object slide down? (m=2 kg, R=0.6 m. Friction is negligible everywhere.)A small object of mass m slides along a slope which is attached tangentially to a cart of mass M. In the middle of the cart a hemicylinder of radius R is attached to the cart as shown in the figure. The small object of mass m just reaches the top point A of this hemicylinder, stops there for an instant, then it falls freely and just hits the rim of the car.

a) At least how long is the cart?

b) What is the mass of the cart?

c) From what height did the small object slide down?

(m=2 kg, R=0.6 m. Friction is negligible everywhere.)

(6 pont)

Deadline expired on January 10, 2013.

Sorry, the solution is available only in Hungarian. Google translation

Megoldásvázlat. Felírható az energiamegmaradás és a vízszintes irányú lendület megmaradásának törvénye, az \(\displaystyle A\) pontot majdnem elérő testre a mozgásegyenlet, valamint az a feltétel, hogy a kényszererő sehol nem lehet húzóerő. Ezekből:

\(\displaystyle a)\) \(\displaystyle L\ge 2{,}4\) m.

\(\displaystyle b)\) \(\displaystyle M \ge 5{,}1\) kg.

\(\displaystyle c)\) \(\displaystyle h\ge 1{,}97~{\rm m}\approx 2~{\rm m}.\)

Statistics:

63 students sent a solution.
6 points:	Balogh Menyhért, Barta Szilveszter Marcell, Csathó Botond, Csordás Gábor, Czipó Bence, Dávid Bence, Filep Gábor, Forrai Botond, Garami Anna, Janzer Barnabás, Kaprinai Balázs, Kollarics Sándor, Kovács 444 Áron, Kovács-Deák Máté, Majoros Péter, Mezősi Máté, Papp Roland, Szabó 928 Attila, Sztilkovics Milán, Varga Blanka.
5 points:	Antalicz Balázs, Baumgartner Róbert, Bingler Arnold, Blum Balázs, Demeter Dániel, Dinev Georgi, Dolecsek 888 Gellért, Farkas Tamás, Fekete Panna, Ferenczi András, Győrfi 946 Mónika, Holczer András, Juhász Iván, Juhász Péter, Kacz Dániel, Krokos Ádám László, Olosz Balázs, Pázmán Zalán, Reitz Angéla, Sági Olivér, Sal Kristóf, Sárvári Péter, Seress Dániel, Sisák Mária Anna, Ürge László, Váli Tamás, Varju Ákos.
4 points:	3 students.
3 points:	4 students.
2 points:	1 student.
1 point:	5 students.
0 point:	3 students.

Problems in Physics of KöMaL, December 2012