Problem P. 4515. (February 2013)

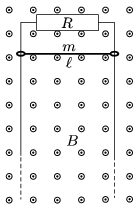
P. 4515. The opposite sides of the vertical conducting frame shown in the figure are parallel, and the top part is connected through a resistor of resistance R=2 ohm. The frame is in uniform magnetic field of B which is perpendicular to the plane of the frame. B=0.8 T. The distance between the parallel, vertical sides of the frame is $\ell$ =20 cm, and the mass of the piece of conductor of negligible resistance, which can slide along the vertical wires without friction is m=200 g. The piece of conductor is released with zero initial speed.

a) Graph the net force exerted on the piece of conductor as a function of the speed of the conductor.

b) Estimate how much time elapses while the speed of the conductor changes from 4 m/s to 4.2 m/s. How much distance does it cover during this?

(5 pont)

Deadline expired on March 11, 2013.

Sorry, the solution is available only in Hungarian. Google translation

Megoldásvázlat. $\displaystyle a)$ $\displaystyle F(v)=mg-\frac{B^2\ell^2}{R}\,v.$

$\displaystyle b)$ Az erő $\displaystyle F(v_1)=1{,}906~{\rm N}$, $\displaystyle F(v_2)=1{,}909~{\rm N}$; alig változik, ezért jó közelítésben az átlagerővel (1,907 N) számolhatunk. $\displaystyle \Delta t=0{,}021~\rm s$, és a megtett út (az átlagsebességből számolva) kb. 8,8 cm.

Statistics:

60 students sent a solution.

5 points: Antalicz Balázs, Asztalos Bogdán, Balogh Menyhért, Barta Szilveszter Marcell, Berezvai Orsolya, Bingler Arnold, Bognár Tamás, Buttinger Milán, Csathó Botond, Csernák Tamás, Cseuz Áron, Czipó Bence, Fehér Zsombor, Filep Gábor, Forrai Botond, Garai Zoltán, Garami Anna, Horváth András Levente, Janzer Barnabás, Juhász Péter, Kacz Dániel, Kaprinai Balázs, Kenderes Anett, Körei Réka, Krokos Ádám László, Lévai 482 Nikolett, Mihály 930 Ákos, Nagy Zsolt, Papp Roland, Pázmán Zalán, Pristyák Levente, Reitz Angéla, Sárvári Péter, Seress Dániel, Szabó 928 Attila, Szilágyi 585 Dezső, Szilágyi András, Sztilkovics Milán, Trócsányi Péter, Vajda Balázs, Váli Tamás.

4 points: 12 students.

3 points: 6 students.

Unfair, not evaluated: 1 solutions.

Problems in Physics of KöMaL, February 2013

60 students sent a solution.
5 points:	Antalicz Balázs, Asztalos Bogdán, Balogh Menyhért, Barta Szilveszter Marcell, Berezvai Orsolya, Bingler Arnold, Bognár Tamás, Buttinger Milán, Csathó Botond, Csernák Tamás, Cseuz Áron, Czipó Bence, Fehér Zsombor, Filep Gábor, Forrai Botond, Garai Zoltán, Garami Anna, Horváth András Levente, Janzer Barnabás, Juhász Péter, Kacz Dániel, Kaprinai Balázs, Kenderes Anett, Körei Réka, Krokos Ádám László, Lévai 482 Nikolett, Mihály 930 Ákos, Nagy Zsolt, Papp Roland, Pázmán Zalán, Pristyák Levente, Reitz Angéla, Sárvári Péter, Seress Dániel, Szabó 928 Attila, Szilágyi 585 Dezső, Szilágyi András, Sztilkovics Milán, Trócsányi Péter, Vajda Balázs, Váli Tamás.
4 points:	12 students.
3 points:	6 students.
Unfair, not evaluated:	1 solutions.

Already signed up?
New to KöMaL?