 Problem P. 4546. (May 2013)
Problem P. 4546. (May 2013)
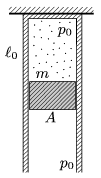
P. 4546. The top part of a thermally insulated, vertical cylinder of cross section A=0.5dm2 is fixed. There is a sample of Helium gas in the cylinder and initially its pressure is p0=105 Pa, its length is  0=50 cm. The bottom part of the cylinder is closed with an initially fixed thermally insulating piston of mass m=10 kg. The external air pressure is also p0. Then the piston is released, and it can move frictionlessly in the cylinder.
0=50 cm. The bottom part of the cylinder is closed with an initially fixed thermally insulating piston of mass m=10 kg. The external air pressure is also p0. Then the piston is released, and it can move frictionlessly in the cylinder.
a) What is the length of the helium confined in the cylinder when the speed of the piston is maximum?
b) What is the maximum speed of the piston?
c) What is the greatest length of the confined gas?
(5 pont)
Deadline expired on June 10, 2013.
Sorry, the solution is available only in Hungarian. Google translation
Megoldásvázlat. \(\displaystyle a)\)
\(\displaystyle \ell_1=\ell_0\left(1-\frac{mg}{p_0A}\right)^{-3/5}=0{,}57~\rm m.\)
\(\displaystyle b)\)
\(\displaystyle v_{\rm max}=\sqrt{\frac{p_0\ell_0A}{m} \left[2\left(\frac{mg}{p_0A}-1\right)\left(\frac{\ell_1}{\ell_0}-1\right)+ 3\left(1-\left(\frac{\ell_0}{\ell_1}\right)^{2/3}\right)\right]}\approx 0{,}8~\frac{\rm m}{\rm s}.\)
\(\displaystyle c)\) \(\displaystyle {\ell_2}/{\ell_0}\equiv \xi\) jelöléssel
\(\displaystyle 3\left(1-\xi^{-2/3}\right)=2\left(\frac{mg}{p_0A}-1\right)(\xi-1),\)
ahonnan \(\displaystyle \xi=1{,}3\); tehát \(\displaystyle \ell_2=0{,}65~\rm m.\)
Statistics:
61 students sent a solution. 5 points: Antalicz Balázs, Balogh Menyhért, Berta Dénes, Bingler Arnold, Blum Balázs, Büki Máté, Csathó Botond, Fehér Zsombor, Fekete Panna, Filep Gábor, Forrai Botond, Garai Zoltán, Holczer András, Janzer Barnabás, Kollarics Sándor, Kovács 444 Áron, Kovács 625 Dorina, Morvay Bálint, Olosz Balázs, Papp Roland, Pristyák Levente, Sal Kristóf, Sárvári Péter, Seress Dániel, Szabó 928 Attila, Sztilkovics Milán, Váli Tamás. 4 points: Buttinger Milán, Csernák Tamás, Dinev Georgi, Jenei Márk, Varju Ákos. 3 points: 7 students. 2 points: 7 students. 1 point: 3 students. 0 point: 10 students. Unfair, not evaluated: 2 solutionss.
Problems in Physics of KöMaL, May 2013
