 Problem P. 4582. (November 2013)
Problem P. 4582. (November 2013)
P. 4582. An astronaut in the International Space-station attaches himself to the four vertices of a regular tetrahedron shaped frame with 4 springs. The mass of the springs and their rest length are negligible, their spring constants are D1=150 N/m, D2=250 N/m, D3=300 N/m and D4=400 N/m. - For the sake of simplicity - the astronaut is considered pointlike, its mass is m=70 kg. What is the period of the oscillation of the astronaut if he is displaced from his equilibrium position and released?
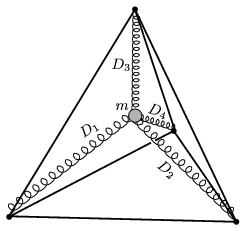
(6 pont)
Deadline expired on December 10, 2013.
Sorry, the solution is available only in Hungarian. Google translation
Megoldásvázlat. \(\displaystyle T=2\pi\sqrt{\frac{m}{D_1+D_2+D_3+D_4}}=1{,}58~\rm s\).
Statistics:
24 students sent a solution. 6 points: Antalicz Balázs, Balogh Menyhért, Bereczki Zoltán, Berta Dénes, Bugár 123 Dávid, Büki Máté, Fehér Zsombor, Holczer András, Horicsányi Attila, Janzer Barnabás, Juhász Péter, Kaposvári Péter, Morvay Bálint, Sal Kristóf, Seress Dániel, Trócsányi Péter, Verasztó Ádám, Zarándy Álmos. 4 points: 1 student. 2 points: 2 students. 0 point: 3 students.
Problems in Physics of KöMaL, November 2013
