Mathematical and Physical Journal
for High Schools
Issued by the MATFUND Foundation
Already signed up?
New to KöMaL?

Problem P. 4587. (December 2013)

P. 4587. A pointlike object of mass m is able to move up and down on a vertical fixed rod. There is a vertical hole at the centre of the object, and the rod fits into this hole, such that the object can slide along the rod frictionlessly. Two pieces of thin light threads are attached to the object, and initially the angle between both threads and the vertical is \alpha=45o. Each thread goes through a pulley, which are at the same height, and at the other end of each thread an object of mass M=1 kg is tied. The system is released from rest.

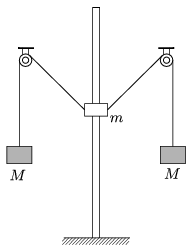
a) What is the mass m of the object on the rod, if after releasing the system it stops at the position where the threads attached to it are horizontal?

b) What is the acceleration of the object of mass m when it starts to move back, and what is the acceleration of the other two objects of mass M, when they start to move back?

(4 pont)

Deadline expired on January 10, 2014.

Sorry, the solution is available only in Hungarian. Google translation

Megoldásvázlat. \(\displaystyle a)\) \(\displaystyle m=2M(\sqrt{2}-1)=\)0,82 kg.

\(\displaystyle b)\) A \(\displaystyle m\) tömegű test \(\displaystyle g\) gyorsulással kezd el esni, a \(\displaystyle M\) tömegű testek gyorsulása ugyanebben a pillanatban nulla.

Statistics:

67 students sent a solution.
4 points:Antalicz Balázs, Bartók Imre, Béda Ármin, Berczi Benjámin, Bereczki Zoltán, Csáky Pál, Demeter Dániel, Di Giovanni Márk, Dombai Tamás, Farkas Tamás, Fehér Zsombor, Fekete Panna, Gróf Tamás, Holczer András, Horváth András Levente, Iván Balázs, Janzer Barnabás, Juhász Péter, Kacz Dániel, Kaposvári Péter, Kasza Bence, Kovács Péter Tamás, Mándoki László, Marosvári Kristóf, Nagy Zsolt, Németh 017 András, Németh Flóra Boróka, Olosz Balázs, Rózsa Tibor, Seress Dániel, Szántó Benedek, Szász Norbert Csaba, Szathmári Balázs, Szentivánszki Soma , Tanner Martin, Varju Ákos, Verasztó Ádám, Zarándy Álmos.
3 points:Balogh Menyhért, Berta Dénes, Biri Eszter Daniela, Dinev Georgi, Kácsor Szabolcs, Koncz Imre, Kormányos Hanna Rebeka, Krokos Ádám László, Pázmán Zalán, Stein Ármin, Turi Soma, Wiandt Péter.
2 points:6 students.
1 point:7 students.
0 point:3 students.
Unfair, not evaluated:1 solutions.

Problems in Physics of KöMaL, December 2013