Problem P. 4588. (December 2013)

P. 4588. A uniform density cube of mass m and of side a is placed to a rough horizontal tray, such that along one of its edge it is placed next to a small bumper. The tray is hung by threads above the centre of mass of the cube at a height of  (see the figure), and then the system is carefully deflected by some angle, as if it was a pendulum, and then released.

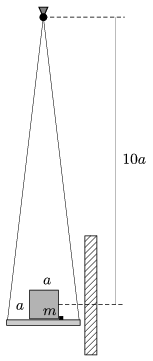
When the pendulum arrives back to its lowermost position, the tray collides with a wall of very big mass. What was the angle of deflection if the cube falls through the bumper? The collisions are totally inelastic. (The masses of the tray and the threads are negligible with respect to the mass of the cube. The moment of inertia of the cube around any axis going through the centre of the cube is ma²/6.)

(5 pont)

Deadline expired on January 10, 2014.

Sorry, the solution is available only in Hungarian. Google translation

Megoldásvázlat. Az energiamegmaradás törvényéből kiszámíthatjuk a kocka ütközés előtti sebességét, és ebből a kocka perdületét. Az ütközéskor a kockára csak az ütközőnél hat nagy erőlökés, tehát ezen pontjára vonatkozó perdülete megmarad. Ha az ütközés utáni mozgási energiája elegendő a tömegközéppontjának megfelelő megemeléséhez, akkor a kocka átbillen. Ennek az a feltétele, hogy a kitérítés szöge \(\displaystyle \alpha>\alpha_{\rm min}\approx 20^\circ\) legyen.

Statistics:

34 students sent a solution.
5 points:	Balogh Menyhért, Berta Dénes, Blum Balázs, Fehér Zsombor, Fekete Panna.
4 points:	Holczer András, Horicsányi Attila, Janzer Barnabás, Olosz Balázs, Trócsányi Péter.
2 points:	2 students.
1 point:	10 students.
0 point:	12 students.

Problems in Physics of KöMaL, December 2013