 Problem P. 4593. (December 2013)
Problem P. 4593. (December 2013)
P. 4593. Two particles whose speeds are very close to the speed of light (ultrarelativistic) collide elastically. The linear momentum vectors of the two particles are shown in the figure. Construct the smallest angle which can be enclosed by the direction of the motion of the two particles flying apart.
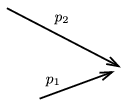
(6 pont)
Deadline expired on January 10, 2014.
Sorry, the solution is available only in Hungarian. Google translation
Megoldásvázlat. A szétrepülő részecskék impulzusának összege \(\displaystyle \boldsymbol p_1+\boldsymbol p_2\), impulzusnagyságaik összege pedig (az energiamegmaradás miatt) \(\displaystyle \vert \boldsymbol p_1\vert+\vert\boldsymbol p_2\vert\) kell legyen. A részecskék impulzusa egy ellipszis valamely pontját a fókuszokkal összekötő vektorral, illetve annak \(\displaystyle -1\)-szeresével adható meg. A kérdéses \(\displaystyle \alpha\) szög akkor a legkisebb, ha az ellipszis pontja a kistengely valamelyik végpontja, és ekkor \(\displaystyle \cos \frac{\alpha}2=\frac{\vert\boldsymbol p_1+\boldsymbol p_2\vert}{\vert \boldsymbol p_1\vert+\vert\boldsymbol p_2\vert}\). Ez a szög a képlet alapján könnyen megszerkeszthető.
Statistics:
13 students sent a solution. 6 points: Asztalos Bogdán, Balogh Menyhért, Blum Balázs, Csathó Botond, Fehér Zsombor, Forrai Botond, Holczer András, Horicsányi Attila, Juhász Péter, Sal Kristóf, Trócsányi Péter. 4 points: 2 students.
Problems in Physics of KöMaL, December 2013
