 Problem P. 4608. (February 2014)
Problem P. 4608. (February 2014)
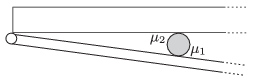
P. 4608. In order that the draught does not slam the door, a flat cylinder shaped object is placed between the door and the threshold, preferably close to the hinge of the door. The symmetry axis is of the cylinder is vertical. To what angle can the draught close the door if the coefficient of kinetic friction between the door and the object is 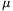 1 and that of between the object and the threshold is
1 and that of between the object and the threshold is 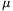 2?
2?
(5 pont)
Deadline expired on March 10, 2014.
Sorry, the solution is available only in Hungarian. Google translation
Megoldásvázlat. Határesetben \(\displaystyle \mu=\tg\frac{\alpha}{2}\), ahol \(\displaystyle \mu\) a két súrlódási együttható közül a kisebb, \(\displaystyle \alpha\) pedig az ajtó és a küszöb hajlásszöge.
Statistics:
39 students sent a solution. 5 points: Balogh Menyhért, Csathó Botond, Fehér Zsombor, Holczer András, Horicsányi Attila, Juhász Péter, Öreg Botond, Sárvári Péter, Tatár Dániel. 4 points: Antalicz Balázs, Fekete Panna, Horváth András Levente, Marosvári Kristóf. 3 points: 3 students. 2 points: 19 students. 1 point: 2 students. 0 point: 2 students.
Problems in Physics of KöMaL, February 2014
