Problem P. 4609. (February 2014)

P. 4609. Both ends of a horizontal thin tube are closed. There is a mercury thread of length h at the middle of the tube. The length of the air columns in both parts is , and the pressure of both air columns is equal to the gauge pressure of a mercury column of height H. The tube is placed to a tumble dryer, the symmetry axis of which is vertical, and the tumble drier is started to spin.

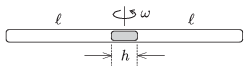
Give the displacement of the mercury thread as a function of the angular speed 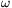, if the temperature is constant.

(5 pont)

Deadline expired on March 10, 2014.

Sorry, the solution is available only in Hungarian. Google translation

Megoldásvázlat. Az elmozdulás \(\displaystyle x=\ell\sqrt{1-\left(\frac{\omega_\text{krit.}}{\omega}\right)^2}\), ha \(\displaystyle \omega>\omega_\text{krit.}=\sqrt{\frac{2gH}{\ell h}},\) egyébként \(\displaystyle x=0\) (tehát a higanyszál nem mozdul ki a középső helyzetéből).

Statistics:

51 students sent a solution.
5 points:	Asztalos Bogdán, Balogh Menyhért, Blum Balázs, Bugár 123 Dávid, Csathó Botond, Fehér Zsombor, Gróf Tamás, Holczer András, Horicsányi Attila, Horváth 974 Bence Attila, Iván Balázs, Janzer Barnabás, Juhász Péter, Kovács Péter Tamás, Sal Kristóf, Wiandt Péter.
4 points:	Antalicz Balázs, Berta Dénes, Dinev Georgi, Farkas Tamás, Forrai Botond, Huszár Emese, Kacz Dániel, Kaposvári Péter, Kasza Bence, Krokos Ádám László, Marosvári Kristóf, Molnár 128 Szilárd, Németh Flóra Boróka, Olosz Balázs, Öreg Botond, Pázmán Zalán, Sárvári Péter, Seress Dániel, Szántó Benedek, Szász Norbert Csaba, Szépfalvi Bálint, Varju Ákos.
3 points:	4 students.
2 points:	4 students.
1 point:	2 students.
0 point:	3 students.

Problems in Physics of KöMaL, February 2014