Problem P. 4620. (March 2014)

P. 4620. A uniform density sphere of radius r=10 cm rolls down with zero initial speed from the top of a hemisphere of radius R=2r. The hemisphere is fixed to a horizontal plane. The coefficient of friction between the two spheres is 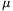=0.2.

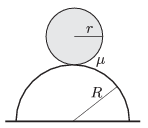
a) Where will the rolling sphere begin to slip?

b) What is the speed of the centre of the sphere at the moment when it begins to slip?

(5 pont)

Deadline expired on April 10, 2014.

Sorry, the solution is available only in Hungarian. Google translation

Megoldásvázlat. \(\displaystyle a)\) A gömb és a félgömb középpontját összekötő egyenes \(\displaystyle 29,1^\circ\)-os szöget zár be a függőlegessel.

\(\displaystyle b)\) \(\displaystyle v=\)0,73 m/s.

Statistics:

57 students sent a solution.
5 points:	Asztalos Bogdán, Balogh Menyhért, Blum Balázs, Bugár 123 Dávid, Csathó Botond, Dinev Georgi, Fekete Panna, Forrai Botond, Holczer András, Horicsányi Attila, Huszár Emese, Iván Balázs, Jakus Balázs István, Janzer Barnabás, Kacz Dániel, Kormányos Hanna Rebeka, Lőrincz Zoltán, Marosvári Kristóf, Németh Flóra Boróka, Pázmán Zalán, Sal Kristóf, Seress Dániel, Szász Norbert Csaba, Varju Ákos, Wiandt Péter.
4 points:	Antalicz Balázs, Ardai István Tamás, Bereczki Zoltán, Fehér Zsombor, Kasza Bence, Kovács Péter Tamás, Krokos Ádám László, Nenezic Patrick Uros, Olosz Balázs, Öreg Botond, Szépfalvi Bálint, Zarándy Álmos.
3 points:	14 students.
2 points:	3 students.
1 point:	2 students.
0 point:	1 student.

Problems in Physics of KöMaL, March 2014