Problem P. 4630. (April 2014)

P. 4630. A sack of sand is lying on a light carpet on a horizontal surface. With the help of the carpet the sack of mass \(\displaystyle M\) is to be pulled from a smooth surface to a rough one. How much work is done if the coefficients of kinetic friction between the surfaces and the carpet are: \(\displaystyle \mu_1\), and \(\displaystyle \mu_2\)? The weight of the sack is not uniform, but we know that the centre of mass of the sack is at a distance of \(\displaystyle s_1\), and \(\displaystyle s_2\) from the ends of the bag.

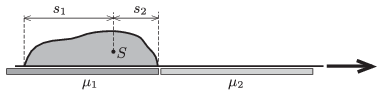
(5 pont)

Deadline expired on May 12, 2014.

Sorry, the solution is available only in Hungarian. Google translation

Megoldásvázlat. \(\displaystyle W=Mg\left(s_2\mu_1+s_1\mu_2\right).\)

Statistics:

39 students sent a solution.
5 points:	Asztalos Bogdán, Balogh Menyhért, Berta Dénes, Blum Balázs, Bugár 123 Dávid, Fehér Zsombor, Forrai Botond, Holczer András, Horicsányi Attila, Janzer Barnabás, Juhász Péter, Kaposvári Péter, Lőrincz Zoltán, Olosz Balázs, Öreg Botond, Rózsa Tibor, Sal Kristóf, Seress Dániel.
3 points:	16 students.
2 points:	1 student.
0 point:	4 students.

Problems in Physics of KöMaL, April 2014