 Problem P. 4643. (May 2014)
Problem P. 4643. (May 2014)
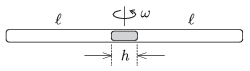
P. 4643. Both ends of a horizontal thin tube are sealed. In the middle of the tube there is a Mercury thread of length \(\displaystyle h\). The length of the air columns in both ends of the tube is \(\displaystyle \ell\), and the pressure of the air in both parts is the gauge pressure of a Mercury column of height \(\displaystyle H\). The tube is put into a centrifuge, which has a vertical axle, and is rotated at an angular speed of \(\displaystyle \omega\).
What can the period of the oscillatory motion of the Mercury column be, provided that the temperature is constant and the oscillation is small? It can also be assumed that \(\displaystyle h\) is small with respect to \(\displaystyle \ell\), so the Mercury column does not break.
(5 pont)
Deadline expired on June 10, 2014.
Sorry, the solution is available only in Hungarian. Google translation
Megoldásvázlat. Ha \(\displaystyle \omega<\omega_\text{krit.}=\sqrt{\frac{2gH}{\ell h}},\) akkor
\(\displaystyle T=2\pi\sqrt{\frac{1}{\omega_\text{krit.}^2-\omega^2}},\)
ha viszont \(\displaystyle \omega>\omega_\text{krit.}\), úgy a rezgésidő
\(\displaystyle T=2\pi \frac{\omega_\text{krit.}}{\omega}\sqrt{\frac{1}{2 ( \omega^2-\omega_\text{krit.}^2)}}.\)
Statistics:
23 students sent a solution. 5 points: Berta Dénes, Fehér Zsombor, Fekete Panna, Holczer András, Horicsányi Attila, Janzer Barnabás. 3 points: 8 students. 2 points: 6 students. 1 point: 3 students.
Problems in Physics of KöMaL, May 2014
