 Problem P. 4675. (November 2014)
Problem P. 4675. (November 2014)
P. 4675. The height of a safe of mass \(\displaystyle M=1000\) kg is \(\displaystyle \ell=1\) m. The safe has a shape of a cube and it has uniform density. The safe is standing on four small legs, in a garage, next to the door of the garage. The coefficient of friction between the legs of the safe and the rough surface of the tiles of the garage is \(\displaystyle \mu_1=0.9\). Outside the garage the ground is a bit smoother, and the coefficient of friction between the ground and the legs is \(\displaystyle \mu_2=0.5\).
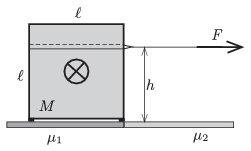
The carrier team uses a horizontal cable at a height of \(\displaystyle h\), and an engine driven winch, to pull out the safe from the garage. The winch (which is to be attached to a strong coloumn) can exert a maximum force of 6000 N. The most-educated (from physics) member of the team states that a stronger winch should be used, because if the weight of the safe is multiplied by the average of the coefficients of friction 7000 N is gained, which exceeds the maximum load of the winch, even if at the beginning with the help of some muscle force two legs of the safe is slid to the smoother ground.
Is the ``Physicist'' of the team right?
(5 pont)
Deadline expired on December 10, 2014.
Statistics:
60 students sent a solution. 5 points: Asztalos Bogdán, Balogh Menyhért, Bencsik Bálint, Berta Dénes, Blum Balázs, Bugár 123 Dávid, Büki Máté, Csathó Botond, Csorba Benjámin, Fehér Balázs, Fekete Balázs Attila, Fekete Gábor, Fekete Panna, Forrai Botond, Fülöp Erik, Gróf Tamás, Holczer András, Jeges Viktor, Juhász 326 Dániel, Kaposvári Péter, Kasza Bence, Kormányos Hanna Rebeka, Kovács Péter Tamás, Körmöczi Dávid, Körtefái Dóra, Molnár 157 Marcell, Molnár Elizabet, Németh 017 András, Németh Flóra Boróka, Olosz Balázs, Orosz Bálint, Páhoki Tamás, Plaszkó Noel, Radnai Bálint, Rózsa Tibor, Sal Kristóf, Szántó Benedek, Szász Norbert Csaba, Szentivánszki Soma , Szirbik Bence, Tompa Tamás Lajos, Varga-Umbrich Eszter, Varju Ákos, Wiandt Péter. 4 points: Nagy Kartal, Südi István, Zarándy Álmos. 3 points: 4 students. 2 points: 4 students. 0 point: 5 students.
Problems in Physics of KöMaL, November 2014
