 Problem P. 4677. (November 2014)
Problem P. 4677. (November 2014)
P. 4677. The figure shows an easily moveable cart, on the top of which there is a slope of angle of elevation of \(\displaystyle \alpha=30^\circ\), which ends in a circular path. The total mass of the cart with the slope is \(\displaystyle M=0.5\) kg. The path is frictionless everywhere. A small pointlike object of mass \(\displaystyle m=0.3\) kg is placed to the top of the slope, which has a height of \(\displaystyle 2R\), and is released without pushing it to any direction.
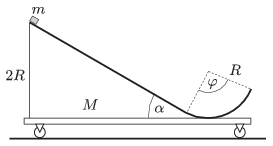
\(\displaystyle a)\) What will the displacement, the velocity and the acceleration of the small object and the cart be, when the small object is at the top of its ascending motion if the central angle of the circular path is \(\displaystyle \varphi=120^\circ\)?
\(\displaystyle b)\) What will the displacement and the velocity of the small object and the cart be at the moment when the small object leaves the circular path if \(\displaystyle \varphi=90^\circ\)?
(5 pont)
Deadline expired on December 10, 2014.
Statistics:
42 students sent a solution. 5 points: Asztalos Bogdán, Balogh Menyhért, Bekes Nándor, Berta Dénes, Blum Balázs, Csathó Botond, Fehér Balázs, Forrai Botond, Fülöp Erik, Holczer András, Jakus Balázs István, Juhász 326 Dániel, Körmöczi Dávid, Nenezic Patrick Uros, Olosz Balázs, Sal Kristóf. 4 points: Bugár 123 Dávid, Di Giovanni Márk, Iván Balázs, Lőrincz Zoltán, Marosvári Kristóf. 3 points: 7 students. 2 points: 10 students. 1 point: 3 students. 0 point: 1 student.
Problems in Physics of KöMaL, November 2014
