Problem P. 4686. (December 2014)

P. 4686. Two alike discs of mass \(\displaystyle m\) and of radius \(\displaystyle R\) touch each other and move with the same velocity perpendicularly to the line segment which joins their centres of mass, along the surface of a horizontal air-cushioned tabletop. There is a third disc of mass \(\displaystyle M\) and of radius \(\displaystyle R\) at rest, at a point on the perpendicular bisector of the line segment joining the centres of mass of the two moving discs. The two moving discs collides totally elastically with the third one, which is at rest. There is no friction between the rims of the discs.

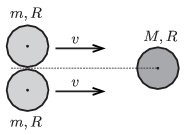
\(\displaystyle a)\) If \(\displaystyle M=m\), what will the speed of the discs be after the collision and what is the direction of their motion?

\(\displaystyle b)\) What should the ratio of \(\displaystyle M/m\) be in order that after the collision the two discs of mass \(\displaystyle m\) move perpendicularly to their initial velocity?

(5 pont)

Deadline expired on January 12, 2015.

Statistics:

42 students sent a solution.
5 points:	Asztalos Bogdán, Balogh Menyhért, Berta Dénes, Blum Balázs, Bugár 123 Dávid, Csathó Botond, Csorba Benjámin, Di Giovanni Márk, Fehér Balázs, Fekete Panna, Forrai Botond, Fülöp Erik, Gróf Tamás, Holczer András, Iván Balázs, Kaposvári Péter, Kormányos Hanna Rebeka, Kovács Péter Tamás, Körmöczi Dávid, Körtefái Dóra, Marosvári Kristóf, Németh Flóra Boróka, Olosz Balázs, Páhoki Tamás, Sal Kristóf, Szántó Benedek, Szász Norbert Csaba, Szentivánszki Soma , Trócsányi Péter.
4 points:	Varju Ákos, Wiandt Péter.
2 points:	1 student.
1 point:	7 students.
0 point:	3 students.

Problems in Physics of KöMaL, December 2014