 Problem P. 4800. (January 2016)
Problem P. 4800. (January 2016)
P. 4800. The electric current in a toroid of mean radius \(\displaystyle R\) is \(\displaystyle I_1\), and its number of turns is \(\displaystyle N_1\). A solenoid of radius \(\displaystyle r\) and of length \(\displaystyle \ell\) (\(\displaystyle \ell\gg R\)), is placed along the symmetry axis of the toroid. The number of turns of the solenoid is \(\displaystyle N_2\). In this coil the current is increased uniformly during a time of \(\displaystyle t_0\), until the magnetic field in the toroid
\(\displaystyle a)\) becomes zero;
\(\displaystyle b)\) becomes the opposite of the original magnetic field in the toroid.
Determine the electric field strength in the toroid along its mean radius in both cases.
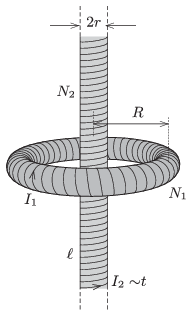
Data: \(\displaystyle R=20\) cm, \(\displaystyle N_1=300\), \(\displaystyle r=4\) cm, \(\displaystyle \ell=2\) m, \(\displaystyle I_1=0.5\) A, \(\displaystyle N_2=4000\), \(\displaystyle t_0=2\) s.
(5 pont)
Deadline expired on February 10, 2016.
Statistics:
19 students sent a solution. 5 points: Asztalos Bogdán, Balogh Menyhért, Bekes Nándor, Blum Balázs, Büki Máté, Forrai Botond, Iván Balázs, Kasza Bence, Kormányos Hanna Rebeka, Kovács Péter Tamás, Németh 777 Róbert, Sal Kristóf, Szentivánszki Soma , Tomcsányi Gergely, Zöllner András. 4 points: Csorba Benjámin, Fekete Balázs Attila, Körmöczi Dávid, Németh Flóra Boróka.
Problems in Physics of KöMaL, January 2016
