 |
A P. 4847. feladat (2016. május) |
P. 4847. Ond egy szabályos háromszög alakú tó partjánál nyaral. Egyszer éppen a háromszög egyik oldalfelezőjénél, a parttól 10 méterre áll, amikor meglátja a túlparton, vele szimmetrikusan napozó barátját, Kondot. Milyen útvonalon kell haladnia Ondnak, hogy mihamarabb odaérhessen a társához, ha a sebessége a szárazföldön 10 km/h, a vízben pedig 2 km/h?
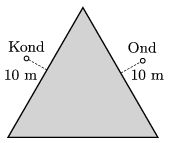
Közli: Forman Ferenc, UK, Cambridge
(4 pont)
A beküldési határidő 2016. június 10-én LEJÁRT.
Megoldás. A feladat optikai megfelelője: Ha létezne \(\displaystyle n=\frac{v_1}{v_2}=5\) törésmutatójú anyag, hogyan juthat el a fény egy ilyen anyagból készített prizma egyik oldaláról a másikra, az Ondnak megfelelő helyről indulva a Kondnak megfelelő helyre? (Az analógia alapja a Fermat-elv, ami a fény terjedési idejének minimumával jellemzi a tényleges fénysugarak pályáját.)
Ha Ond valameddig a parton fut, majd a vízben halad tovább, és a túlsó parton ismét szaladva éri el Kondot, akkor a vízben megtett útjának iránya a partra merőleges egyenessel (az optikai analógia szerint) legfeljebb
\(\displaystyle \beta_1=\arcsin \frac{\sin\alpha_1}{n}\le \arcsin \frac{1}{5}=11{,}5^\circ\)
és
\(\displaystyle \beta_2=\arcsin \frac{\sin\alpha_2}{n}\le \arcsin \frac{1}{5}=11{,}5^\circ\)
lehet.
Ez azonban nem lehetséges, mert az ábrán látható kisebb háromszög szögeinek összege:
\(\displaystyle (90^\circ-\beta_1)+(90^\circ-\beta_2)+60^\circ=180^\circ,\)
azaz \(\displaystyle \beta_1+\beta_2=60^\circ\).
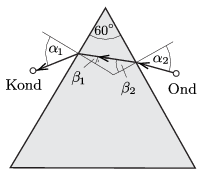
A fény tehát nem juthat el \(\displaystyle -\) a fénytörés törvényeit követve \(\displaystyle -\) Ond helyétől Kond helyéig. (Érdekes, hogy ez az állítás nem függ a fény kiindulási és érkezési pontjától, bármilyen két pontra érvényes, amennyiben azok nem köthetők össze egy \(\displaystyle -\) a prizmát kikerülő \(\displaystyle -\) egyenessel.) Visszatérve az eredeti feladathoz: Ond úgy juthat el a leghamarabb Kondhoz, ha megkerüli a tavat, tehát egyenesen fut a háromszög ,,felső'' csúcsáig, és onnan tovább egyenesen a barátjáig.
Statisztika:
30 dolgozat érkezett. 4 pontot kapott: Ardai István Tamás, Bartók Imre, Blum Balázs, Bukor Benedek, Conrád Márk, Csorba Benjámin, Debreczeni Tibor, Elek Péter, Farkas Domonkos, Fehér 169 Szilveszter, Fehér Aliz, Kárpáti Kristóf, Kárpáti Márton, Kluèka Vivien, Kuchár Zsolt, Makovsky Mihály, Mány Bence, Molnár Mátyás, Nagy Nándor, Németh 777 Róbert, Németh Csaba Tibor, Olosz Adél, Osváth Botond, Szántó Benedek, Szentivánszki Soma , Tófalusi Ádám. 2 pontot kapott: 2 versenyző. 1 pontot kapott: 1 versenyző. 0 pontot kapott: 1 versenyző.
A KöMaL 2016. májusi fizika feladatai

