Problem P. 4860. (September 2016)

P. 4860. Two fixed, point-like charges of charge \(\displaystyle q\) are found at the endpoints of a horizontal line segment of length \(\displaystyle 2d\). A ball of mass \(\displaystyle m\) and of charge \(\displaystyle Q\) is dropped from point \(\displaystyle P_1\) which is on the vertical, perpendicular bisector of the line segment. The ball stops exactly at point \(\displaystyle P_2\).

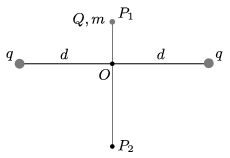
\(\displaystyle a)\) What is the mass of the ball?

\(\displaystyle b)\) What is the acceleration of the ball at point \(\displaystyle P_2\)?

Data: \(\displaystyle q=2\cdot 10^{-6}\) C, \(\displaystyle Q=-6\cdot 10^{-6}\) C, \(\displaystyle d=12\) cm, \(\displaystyle OP_1=5\) cm, \(\displaystyle OP_2=10\) cm.

(4 pont)

Deadline expired on October 10, 2016.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. \(\displaystyle a)\) A golyó távolsága a töltésektől kezdetben \(\displaystyle r_1= 0{,}13\) m, a \(\displaystyle P_2\) pontban pedig \(\displaystyle r_2=0{,}156\) m. A golyó \(\displaystyle h=0{,}15\) m-nyi süllyedése során a gravitációs és az elektrosztatikus energiaváltozásának összege (a munkatétel szerint) nulla, így

\(\displaystyle 2kQq\left(\frac{1}{r_2}-\frac{1}{r_2}\right)-mgh=0.\)

Innen a megadott számadatokkal \(\displaystyle m=0{,}19~\)kg.

\(\displaystyle b)\) A \(\displaystyle P_2\) pontban függőlegesen felfelé ható erő:

\(\displaystyle F=2kq\vert Q\vert \frac{H}{r_2^3}-mg,\)

ahol \(\displaystyle H=OP_2=0{,}1~\)m. Innen a már kiszámított tömeg ismeretében a gyorsulás (felfelé):

\(\displaystyle a=\frac{F}{m}= 20{,}1~ {\rm m}/{\rm s^2}.\)

Statistics:

74 students sent a solution.
4 points:	Ardai István Tamás, Balaskó Dominik, Balog 518 Lóránd, Bartók Imre, Bekes Nándor, Berke Martin, Csenger Géza, Csire Roland, Csóka987 Benedek, Csuha Boglárka, Debreczeni Tibor, Di Giovanni András, Édes Lili, Elek Péter, Eper Miklós, Facskó Benedek, Faisal Fahad AlSallom, Fajszi Bulcsú, Fehér 169 Szilveszter, Fekete Balázs Attila, Guba Zoltán, Hanusz Fruzsina, Illés Gergely, Illyés András, Iván Balázs, Jáger Balázs, Jakus Balázs István, Kolontári Péter, Krasznai Anna, Markó Gábor, Marozsák Tóbiás , Merkl Gergely, Mocskonyi Mirkó, Molnár 957 Barnabás, Németh 123 Balázs, Nenezic Patrick Uros, Ónodi Gergely, Osváth Botond, Páhoki Tamás, Papp 121 Krisztina, Paulovics Péter, Pszota Máté, Riskutia Balázs, Schmera Dániel, Tibay Álmos, Tófalusi Ádám, Tóth 111 Máté , Tóth 420 Péter, Zöllner András, Zsombó István.
3 points:	10 students.
2 points:	8 students.
1 point:	5 students.
0 point:	1 student.

Problems in Physics of KöMaL, September 2016