Problem P. 4865. (October 2016)

P. 4865. Two cars are undergoing uniform straight line motion along two straight motorways, which are perpendicular to each other, as shown in the figure. Initially the vehicles were at a distance of \(\displaystyle x_0=6\) km and \(\displaystyle y_0=3\) km from the cross-roads. The speed of the car moving along the path labelled \(\displaystyle AO\) is \(\displaystyle v_1=36~\)km/h. It takes 9 minutes for the cars to reach the position where they are the closest to each other during their motion.

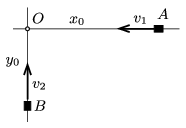
What is the speed of the car travelling along path \(\displaystyle BO\), and what is the shortest distance between them?

(5 pont)

Deadline expired on November 10, 2016.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. I. (algebrai) megoldás. A két gépkocsi közötti távolság négyzete \(\displaystyle t\) idejű mozgás után:

\(\displaystyle d^2=(x_0-v_1t)^2+(y_0-v_2t)^2= \left(t\sqrt{v_1^2+v_2^2}-\frac{v_1x_0+v_2y_0}{\sqrt{v_1^2+v_2^2}}\right)^2+ x_0^2+y_0^2-\frac{(v_1x_0+v_2y_0)^2}{v_1^2+v_2^2}.\)

Ez a kifejezés akkor a legkisebb, amikor

\(\displaystyle t=\frac{ v_1x_0+v_2y_0 }{v_1^2+v_2^2}.\)

Ez \(\displaystyle v_2\)-re nézve egy másodfokú egyenlet, amelynek (pozitív) megoldása: \(\displaystyle v_2^{(1)}=25{,}6~\rm km/h\), és a hozzá tartozó minimális távolság: \(\displaystyle d_\text{min}^{(1)}=1{,}03~\rm km.\)

A fentebbi másodfokú egyenletnek van egy másik, a \(\displaystyle v_2<0\) tartományba eső megoldása is. Fizikailag ez annak felel meg, hogy a \(\displaystyle B\) pontban lévő jármű távolodik a kereszteződéstől: \(\displaystyle v_2^{(2)}=-5{,}62~{\rm km/h}\) és \(\displaystyle d_\text{min}^{(2)}=3{,}9~\rm km.\)

II. (geometriai) megoldás. Írjuk le a mozgást a \(\displaystyle B\) járműből (annak vonatkoztatási rendszeréből) nézve. Ebben a leírásban a \(\displaystyle B\) jármű áll, a másik pedig a \(\displaystyle (-v_1,v_2)\) vektorral jellemezhető (most még ismeretlen) irányban mozog (lásd az ábrát). (A vektor komponenseit az \(\displaystyle OA\), illetve az \(\displaystyle OB\) irányban tekintjük pozitívnak.)

Ha a két jármű \(\displaystyle t\) idő múlva kerül egymáshoz legközelebb, akkor ezen pillanatban az \(\displaystyle A\) pontból induló jármű távolsága az \(\displaystyle OB\) egyenestől \(\displaystyle x_0-v_1t\) lesz, vagyis a jármű a szaggatott vonallal jelölt egyenes valamelyik pontjába kerül.

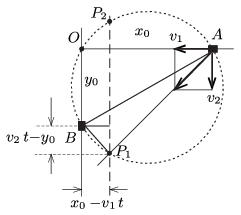
Másrészt a kérdéses pontban a két jármű közötti távolság minimális, tehát a relatív sebességük merőleges a járműveket összekötő egyenesre. Ezek szerint a kérdéses pont rajta fekszik az \(\displaystyle AB\) szakaszhoz tartozó Thalész-körön. Az ábrán látszik, hogy két ilyen pont is lehetséges, a \(\displaystyle v_2>0\)-hoz tartozó \(\displaystyle P_1\) pont, illetve a \(\displaystyle v_2<0\)-hoz tartozó \(\displaystyle P_2\) pont. A megfelelő derékszögű háromszögek hasonlóságát kihasználva felírhatjuk, hogy

\(\displaystyle \frac{v_1}{v_2}=\frac{v_2t-y_0}{x_0-v_1t},\)

ahonnan az ismert adatok behelyettesítése után a (km/h egységekben felírt) \(\displaystyle v_2\)-re ezt a másodfokú egyenletet kapjuk:

\(\displaystyle v_2^2-20v_2-144=0,\)

aminek a megoldásai: 25,6 és \(\displaystyle -5{,}6\), és ezek ismeretében a két jármű kérdezett távolsága is kiszámítható az egyes esetekben: \(\displaystyle BP_1=1{,}0~\rm km\), illetve \(\displaystyle BP_2=3{,}9~\rm km\)

Statistics:

125 students sent a solution.
5 points:	66 students.
4 points:	6 students.
3 points:	4 students.
2 points:	18 students.
1 point:	22 students.
0 point:	5 students.
Unfair, not evaluated:	4 solutionss.

Problems in Physics of KöMaL, October 2016