A P. 4866. feladat (2016. október)

P. 4866. Két, egyenként \(\displaystyle \ell\) hosszúságú fonálinga függ egymás mellett úgy, hogy a fonalak végén lévő golyók az ábrán látható módon összeérnek. Az egyik golyó \(\displaystyle M\) tömege sokkal nagyobb a másik golyó \(\displaystyle m\) tömegénél.

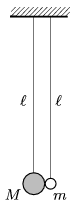
\(\displaystyle a)\) Kissé kitérítjük a bal oldali ingát úgy, hogy a \(\displaystyle M\) tömegű golyó emelkedése \(\displaystyle h\ll \ell\) legyen, azután elengedjük. A két golyó rugalmas ütközése után legfeljebb milyen magasra emelkedhet fel a \(\displaystyle m\) tömegű golyó?

\(\displaystyle b)\) Ha mindkét ingát kitérítjük ellentétes irányban úgy, hogy mindkét golyó emelkedési magassága \(\displaystyle h\ll \ell\) legyen, akkor a rugalmas ütközés után milyen maximális magasságba emelkedik fel a \(\displaystyle m\) tömegű golyó?

Közli: Lambodara Mishra, Ahmedabad, India

(4 pont)

A beküldési határidő 2016. november 10-én LEJÁRT.

Megoldás. \(\displaystyle a)\) Az ütközést megelőző pillanatban a \(\displaystyle M\) tömegű golyó sebessége \(\displaystyle v=\sqrt{2gh}\), a másik golyó áll. Ha az ütközést a \(\displaystyle M\) tömegű golyóhöz rögzített koordináta-rendszerből szemléljük, a nagyobb tömegű golyót állónak, a másikat \(\displaystyle -v\) sebességgel mozgónak látjuk. Az ütközés után a kis golyó sebessége \(\displaystyle +v\)-re változik, ami az eredeti (álló) koordináta-rendszerből szemlélve \(\displaystyle 2v\) sebességnek felel meg. A kis golyó legnagyobb emelkedési magasságát (\(\displaystyle h_1\)-et) az energiatételből kaphatjuk meg:

\(\displaystyle \frac12 m(2v)^2= mgh_1,\qquad \text{azaz}\qquad h_1=\frac{2v^2}{g}=4h.\)

\(\displaystyle b)\) Az ütközés előtt mindkét golyó \(\displaystyle v=\sqrt{2gh}\) nagyságú, egymással ellentétes irányú sebességgel mozog. A nagy golyóhoz rögzített koordináta-rendszerből nézve a kis golyó sebessége \(\displaystyle -2v\), ami az ütközés után \(\displaystyle +2v\)-re változik. Az álló koordináta-rendszerben ez \(\displaystyle 3v\) sebességnek felel meg, amihez \(\displaystyle h_2=9h\) emelkedési magasság tartozik.

A megoldás (mindkét esetben) akkor is érvényes marad, ha a kezdeti kitérés nem lenne kicsi, de a közegellenállás még elhanyagolható.

Statisztika:

59 dolgozat érkezett.
4 pontot kapott:	Balaskó Dominik, Balog 518 Lóránd, Berke Martin, Bukor Benedek, Csóka987 Benedek, Csuha Boglárka, Elek Péter, Fehér 169 Szilveszter, Fekete Balázs Attila, Hajnal Dániel Konrád, Illés Gergely, Iván Balázs, Karl János, Kiss Dániel Márk, Klučka Vivien, Kolontári Péter, Krasznai Anna, Magyar Róbert Attila, Markó Gábor, Mocskonyi Mirkó, Molnár Mátyás, Morvai Orsolya, Nagy 555 Botond, Németh 777 Róbert, Németh Csaba Tibor, Olosz Adél, Páhoki Tamás, Papp 121 Krisztina, Pataki 245 Attila, Póta Balázs, Sallai Krisztina, Tófalusi Ádám, Turcsányi Ádám.
3 pontot kapott:	Ardai István Tamás, Bege Áron, Fajszi Bulcsú, Illyés András, Molnár 957 Barnabás, Sal Dávid, Takács Attila, Varga-Umbrich Eszter.
2 pontot kapott:	7 versenyző.
1 pontot kapott:	6 versenyző.
0 pontot kapott:	5 versenyző.

A KöMaL 2016. októberi fizika feladatai