Problem P. 4875. (November 2016)

P. 4875. A uniform-density hemisphere is placed onto a rough inclined plane of small elevation angle, and then the angle of elevation is slowly increased.

\(\displaystyle a)\) Determine the angle of elevation of the slope when the hemisphere just slips on the incline if the coefficient of static friction is 0.3. Does this angle depend on whether the hemisphere is put onto the plane with its convex or plain part?

\(\displaystyle b)\) What is the angle between the slope and the plane part of the hemisphere at the moment when the hemisphere starts to slide if it is placed on the slope with its convex part?

Hereafter suppose that the coefficient of friction between the slope and the hemisphere is much greater than the value given above. Two different types of experiments are done: the hemisphere is placed on the slope such that first the convex, then the plane part of the object touches the slope. The angle of elevation of the slope is slowly increased in both cases.

\(\displaystyle c)\) What may the maximum value of the slope angle be in each case in order that the hemisphere stays at rest? What is the least value of the coefficient of static friction in each case in order to reach the critical angle of elevation?

(5 pont)

Deadline expired on December 12, 2016.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Táblázati adatok szerint (lásd pl. a ,,Négyjegyű'' 198. oldalán az üreges félgömbre vonatkozó képletet) egy \(\displaystyle R\) sugarú homogén félgömb tömegközéppontja a geometriai középpontjától \(\displaystyle \tfrac38 R\) távolságban, a szimmetriatengelyén található.

\(\displaystyle a)\) A lejtőre helyezett – akármilyen alakú – merev test akkor csúszik meg, amikor a lejtő esésvonalával párhuzamos \(\displaystyle S\) súrlódási erő nagysága eléri a lejtőre merőleges \(\displaystyle N\) nyomórő \(\displaystyle \mu\)-szörösét, esetünkben 0,3-szorosát. Mivel az erőegyensúly feltételei miatt \(\displaystyle S=mg\sin\alpha\) és \(\displaystyle N=mg\cos\alpha\) (ahol \(\displaystyle \alpha\) a lejtő hajlásszöge, \(\displaystyle mg\) pedig a test súlya), a megcsúszás határszögére a \(\displaystyle \tg\alpha_0=0{,}3\) feltétel érvényes, ahonnan \(\displaystyle \alpha_0=16{,}7^\circ\). Ez az eredmény (amely csak a megcsúszás határhelyzetére vonatkozik) független attól, hogy melyik felével helyeztük a félgömböt a lejtőre. A továbbiakban vizsgálni kell még azt is, hogy vajon nem borul-e fel a test egy ilyen meredek lejtőn.

\(\displaystyle b)\) A domború oldalával lefelé álló félgömb csak akkor maradhat egyensúlyban a lejtőn, ha a \(\displaystyle C\) tömegközéppontja a lejtővel érintkező \(\displaystyle P\) pontja felett, azon átmenő függőleges egyenesen helyezkedik el. (Ellenkező esetben a súlyerőnek lenne az érintkezési pontra vonatkoztatott forgatónyomatéka, és emiatt a test elfordulna és felborulna). Ez a feltétel úgy valósulhat meg, hogy a félgömb síklapja a lejtő síkjához képest valamekkora \(\displaystyle \varphi\) szöggel elfordul.

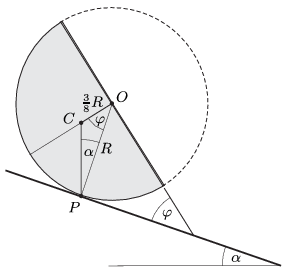
1. ábra

Az \(\displaystyle OPC\) háromszögre felírhatjuk a szinusztételt:

\(\displaystyle \frac{\sin\alpha}{\sin(\alpha+\varphi)}=\frac{3}{8},\)

ahonnan a megcsúszás \(\displaystyle \alpha=\alpha_0\) határszögénél (\(\displaystyle \mu=0{,}3\) esetén) a kérdéses szögre \(\displaystyle \varphi=33{,}3^\circ\) adódik.

\(\displaystyle c)\) Ha a tapadó súrlódási együttható az előzőnél nagyobb érték, akkor \(\displaystyle \alpha\) és vele együtt \(\displaystyle \varphi\) nagyobb is lehet, mint a fentebb kiszámított szög. De \(\displaystyle \alpha\) növelésével, ha

\(\displaystyle \sin\alpha>\frac{3}{8},\qquad \text{vagyis}\qquad \alpha>\alpha_1=22,0^\circ,\)

a szinusztételt kihasználó egyenletnek nincs megoldása \(\displaystyle \varphi\)-re, vagyis a félgömbnek nincs olyan egyensúlyi helyzete, amelynél a domború felével érintkezik a lejtővel; a félgömb tehát felborul. A határesetnek megfelelő szögnél a súrlódási együttható szükséges nagysága: \(\displaystyle \mu_1=\tg\alpha_1=0{,}40.\)

Amennyiben a félgömböt a sík felével helyezzük a lejtőre, majd növeljük a lejtő hajlásszögét, a félgömb ebből a helyzetéből is felborulhat, ha a tömegközéppontján átmenő függőleges egyenes a lejtővel érintkező körlapon kívülre kerül. A határesetnek megfelelő hajlásszög a \(\displaystyle \tg\alpha=\frac{8}{3}\) feltételből (2. ábra) \(\displaystyle \alpha=\alpha_2=69{,}4^\circ\) és a kritikus súrlódási együttható \(\displaystyle \mu_2=\tg\alpha_2=2{,}67.\)

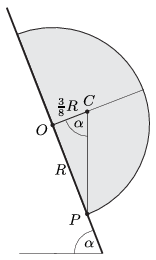
2. ábra

Az \(\displaystyle a)\) kérdésben szereplő \(\displaystyle \alpha_0\) szög kisebb, mint \(\displaystyle \alpha_1\) és \(\displaystyle \alpha_2\), tehát a félgömb sem a síklapjáról, sem pedig a domború oldaláról nem borulhat fel, mielőtt megcsúszna.

Statistics:

40 students sent a solution.
5 points:	Bekes Nándor, Di Giovanni András, Mamuzsics Gergő Bence, Marozsák Tóbiás , Németh 777 Róbert, Tófalusi Ádám.
4 points:	Fehér 169 Szilveszter, Jakus Balázs István, Mocskonyi Mirkó.
3 points:	19 students.
2 points:	5 students.
1 point:	6 students.
0 point:	1 student.

Problems in Physics of KöMaL, November 2016