Problem P. 4876. (November 2016)

P. 4876. The area of the inner cross section of the left part of a horizontal fixed tube is \(\displaystyle A\), whilst the area of the cross section of its part on the right hand-side is \(\displaystyle kA\), where \(\displaystyle k<1\) (e.g. \(\displaystyle k=\frac{1}{5})\). The two parts are attached smoothly without any sharp turns as shown in the figure. In the tube there is some liquid of density \(\displaystyle \varrho\) and of negligible viscosity. With the help of a piston at the left hand-side, the liquid can be pushed out of this part of the tube. The water which leaves the tube hits a vertical wall and spreads out, creating a tapering film of fluid.

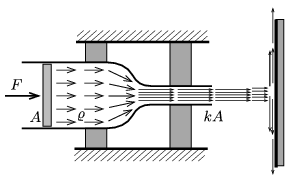
\(\displaystyle a)\) At what constant speed does the piston move if the external force exerted on it has a constant value of \(\displaystyle F\)?

\(\displaystyle b)\) What is the force exerted by the water on the vertical wall?

\(\displaystyle c)\) What is the value of the horizontal force which is exerted by the tube on the fastening?

Suppose that the flow is constant in time (stationary), and that the effect of gravity can be neglected in the problem.

(6 pont)

Deadline expired on December 12, 2016.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. A dugattyú viszonylag hamar (jó közelítéssel) egyenletesen fog mozogni. (Ez annál hamarabb következik be, minél kisebb \(\displaystyle k\) értéke. Ha \(\displaystyle k\rightarrow 1\), akkor nem alakul ki egyenletes mozgás, a dugattyú és a víz egyenletesen gyorsul.)

\(\displaystyle a)\) Jelöljük a dugattyú állandósult sebességét \(\displaystyle v\)-vel. A cső jobb oldali végénél kiáramló folyadék sebessége (a folyadék összenyomhatatlansága miatt) \(\displaystyle v/k\) lesz.

Tekintsük az áramló folyadékot valamelyik időpillanatban, illetve egy kicsiny \(\displaystyle \Delta t\) idővel később. A dugattyú elmozdulása ezalatt \(\displaystyle v\Delta t\), a külső erő munkája tehát

\(\displaystyle W=Fv\Delta t.\)

A csőből kiáramló folyadék tömege \(\displaystyle \Delta m=\varrho Av\Delta t\), sebessége \(\displaystyle v/A\), a teljes mozgási energia változása tehát

\(\displaystyle \Delta E=\frac{1}{2}\Delta m \left(\frac{v}{k}\right)^2-\frac{1}{2}\Delta m v^2.\)

(Úgy számolhatunk, mintha a dugattyú melletti \(\displaystyle \Delta m\) tömegű folyadékmennyiség \(\displaystyle v\) sebességről \(\displaystyle v/k\) sebességre gyorsult volna fel, és a folyadék többi részének sebessége nem változott volna.)

A munkatétel szerint \(\displaystyle W=\Delta E\), ahonnan

\(\displaystyle v=\sqrt{\frac{F}{\varrho A}\,\frac{2k^2}{1-k^2}}.\)

Ha például \(\displaystyle k=\tfrac{1}{5}\), akkor

\(\displaystyle v=\sqrt{\frac{F}{12\varrho A}}\approx 0{,}29\sqrt{\frac{F}{ \varrho A}}.\)

A dugattyú sebességét a

\(\displaystyle p+\varrho\frac{v^2}{2}+\varrho gh\)

Bernoulli-törvény felhasználásával is megkaphatjuk. A dugattyú közelében a folyadék nyomása \(\displaystyle p_0+\frac{F}{A}\), az áramlás sebessége pedig \(\displaystyle v\). A kiáramló folyadék nyomása a \(\displaystyle p_0\) külső légnyomással egyezik meg, sebessége pedig \(\displaystyle v/k\). A \(\displaystyle \varrho gh\) tag a gravitáció figyelmen kívül hagyása miatt nulla. Így

\(\displaystyle p_0+\frac{F}{A}+\frac{\varrho}{2}v^2=p_0+\frac{\varrho}{2} \,\frac{v^2}{k^2},\)

tehát

\(\displaystyle v=\sqrt{\frac{F}{\varrho A}\,\frac{2k^2}{1-k^2}}.\)

A munkatételből és a Bernoulli-törvényből kapott eredmény megegyezik, ami nem meglepő, hiszen a Bernoulli-törvény éppen a mechanikai energia megmaradását fejezi ki a folyadékok áramlásakor.

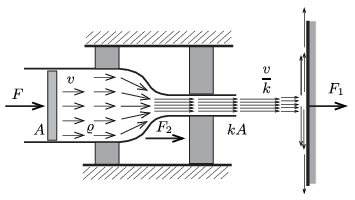
\(\displaystyle b)\) Ha a függőleges falnak csapódó víz \(\displaystyle F_1\) nagyságú, jobbra mutató erőt fejt ki a falra, akkor a fal ugyanekkora nagyságú, balra mutató erővel hat a folyadékra. Mivel \(\displaystyle \Delta t\) idő alatt \(\displaystyle \Delta m\) tömegű, \(\displaystyle v/k\) sebességű folyadék veszíti el vízszintes irányú lendületét, fennáll

\(\displaystyle -F_1\Delta t= -(\varrho A v \Delta t) \frac{v}{k},\)

vagyis (\(\displaystyle v\) korábban kiszámított értékét felhasználva)

\(\displaystyle F_1=\frac{2k}{1-k^2}\,F=\frac{5}{12}F\approx 0{,}42\, F. \)

\(\displaystyle c)\) A cső rögzítésére ható \(\displaystyle F_2\) erőt ugyancsak a lendületváltozás tételéből határozhatjuk meg. A folyadéknak a csőben lévő részére \(\displaystyle F-F_2\) erő hat, ezt a dugattyú, illetve a folyadéknyomásból származó, a szűkület falára ható erő ellenereje fejti ki. A lendületváltozás egyenlete:

\(\displaystyle \left(F-F_2\right)=\Delta m\left( \frac{v}{k}-v\right),\)

ahonnan

\(\displaystyle F_2=\frac{1-k}{1+k}\,F=\frac{2}{3}\,F\approx 0{,}67\,F.\)

Megjegyzés: Figyelemre méltó, hogy \(\displaystyle F_1+F_2\ne F\), de ez nem ellentmondás, hiszen (a sebességek időbeli állandósága ellenére) a teljes folyadékmennyiség lendülete időben egyre változik, csökken. Az eredő erő

\(\displaystyle F-F_1-F_2= -\frac{2k^2}{1-k^2}\,F\)

és ez éppen megegyezik a

\(\displaystyle \frac{\Delta I_\text{összes}}{\Delta t}= -\frac{\Delta m\cdot v }{\Delta t}=-\varrho A v^2\)

mennyiséggel, összhangban Newton II. törvényével.

Statistics:

44 students sent a solution.
6 points:	Bartók Imre, Bekes Nándor, Di Giovanni András, Fajszi Bulcsú, Fehér 169 Szilveszter, Fekete Balázs Attila, Illés Gergely, Jakus Balázs István, Kavas Katalin, Marozsák Tóbiás , Nagy 555 Botond, Németh 777 Róbert, Olosz Adél, Páhoki Tamás, Sal Dávid, Szentivánszki Soma , Tófalusi Ádám.
5 points:	Elek Péter.
4 points:	2 students.
3 points:	7 students.
2 points:	4 students.
1 point:	2 students.
0 point:	11 students.

Problems in Physics of KöMaL, November 2016