 Problem P. 4877. (November 2016)
Problem P. 4877. (November 2016)
P. 4877. A double cylinder, made of some good conducting material, can move with the help of the wheels attached to it. The wall of the cylinders have negligible width, and the areas of the inner cross section of the cylinders are \(\displaystyle A_1\) and \(\displaystyle A_2\). In the cylinders there are pistons, which are attached to walls. The distance between the pistons and the plane along which the two cylinders touch each other is \(\displaystyle L\). In the confined region there is a sample of oxygen gas at a temperature of \(\displaystyle T_0\). The ambient air pressure is \(\displaystyle p_0\).
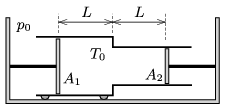
The temperature is slowly increased to \(\displaystyle T_1\).
\(\displaystyle a)\) By what amount does the double cylinder move during the temperature change?
\(\displaystyle b)\) How much heat is absorbed by the oxygen gas in the heating process?
(Data: \(\displaystyle A_1=10~\rm cm^2\), \(\displaystyle A_2=5~\rm cm^2\), \(\displaystyle L=10~\rm cm\), \(\displaystyle p_0=100\) kPa, \(\displaystyle T_0=250\) K, \(\displaystyle T_1=300\) K.)
(4 pont)
Deadline expired on December 12, 2016.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. A kettős hengerre (a hengerek érintkezési felületénél) a külső és a belső nyomás különbségével arányos erő hat. Mivel a kettős henger a kerekeken könnyen el tud mozdulni, ez az erő nulla, vagyis a külső és a belső nyomás megegyezik.
\(\displaystyle a)\) Az izobár állapotváltozás során a gáz térfogata a kezdeti \(\displaystyle V_0=A_1L+A_2L=150~\rm cm^3\) értékről
\(\displaystyle V_1=V_0\frac{T_1}{T_0}=180~\rm cm^3\)
nagyságúra változik, tehát \(\displaystyle 30~\rm cm^3\)-rel megnő. A kettős henger tehát a melegítés során 6 cm-t mozdul el (jobbra).
\(\displaystyle b)\) A felvett hő az I. főtétel szerint
\(\displaystyle Q=\Delta E+p\Delta V=\frac{5}{2}(p_0V_1-p_0V_0)+p_0(V_1-V_0)=\frac{7}{2}p_0(V_1-V_0)=10{,}5~\rm J.\)
Statistics:
82 students sent a solution. 4 points: 56 students. 3 points: 19 students. 2 points: 5 students. 1 point: 2 students.
Problems in Physics of KöMaL, November 2016
