 Problem P. 4880. (November 2016)
Problem P. 4880. (November 2016)
P. 4880. At the centre of a solenoid of diameter \(\displaystyle d=4.4\) cm, of length \(\displaystyle \ell=1\) m and of \(\displaystyle N=1000\) number of turns, there is a thick, circular, conducting coaxial ring. The ring has a radius of \(\displaystyle r=2.5\) cm, and its resistance is \(\displaystyle R=10^{-4}~\Omega\). The \(\displaystyle 50\) A current in the solenoid is changed to \(\displaystyle -50\) A in 1 second.
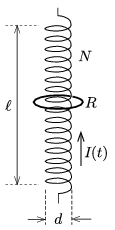
\(\displaystyle a)\) What is the magnitude of the magnetic induction at the centre of the ring when the current in the solenoid is zero?
\(\displaystyle b)\) What is this value \(\displaystyle \Delta t=0.001\) s before and after the above described moment?
(5 pont)
Deadline expired on December 12, 2016.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. A tekercsben folyó, időben változó nagyságú áram által létrehozott mágneses fluxus:
\(\displaystyle \Phi(t)=\mu_0\frac{N I(t)}{\ell}\cdot \frac{d^2\pi}{4},\)
így a körvezető gyűrűben indukált feszültség nagysága
\(\displaystyle U=\frac{\Delta\Phi}{\Delta t}=\mu_0\frac{N d^2\pi}{4\ell}\cdot \frac{\Delta I(t)}{\Delta t}, \)
aminek hatására abban
\(\displaystyle I'=\frac{U}{R}=\mu_0\frac{N d^2\pi}{4\ell R}\cdot \frac{\Delta I(t)}{\Delta t}\)
áram indul meg. Az \(\displaystyle I(t)\) áram változási sebességének nagysága:
\(\displaystyle \left\vert\frac{\Delta I(t)}{\Delta t}\right\vert=100~\frac{\rm A}{\rm s}.\)
Mivel \(\displaystyle I(t)\) időben egyenletesen változik, \(\displaystyle U\) és \(\displaystyle I'\) is időben állandó, tehát a körvezetőnél önindukciós jelenséggel nem kell számolnunk.
\(\displaystyle a)\) Abban a pillanatban, amikor \(\displaystyle I(t)=0\), a tekercs saját mágneses tere is nulla, a körvezetőben folyó áram viszont a gyűrű középpontjában
\(\displaystyle B'=\mu_0\frac{I'}{2r}=\mu_0^2\frac{N d^2\pi}{8\ell rR}\cdot \frac{\Delta I(t)}{\Delta t}= \frac{(12{,}6\cdot10^{-7})^2\cdot 10^3\cdot 0{,}044^2\,\pi\cdot 10^2}{8\cdot 0{,}025\cdot 10^{-5}}~{\rm T}=0{,}05 ~{\rm mT} \)
nagyságú mágneses indukciót hoz létre.
\(\displaystyle b)\) A tekercsben folyó áram erőssége a kérdéses pillanatokban
\(\displaystyle I_1=\pm 100~\frac{\rm A}{\rm s}\cdot \Delta t=\pm 0{,}1~\rm A.\)
Ekkora áram a tekercs középpontjában
\(\displaystyle B= \mu_0\frac{N I_1}{\ell}=\pm 0{,}13~{\rm mT} \)
mágneses indukciót eredményez. (A tekercs által keltett mágneses indukció a tekercs tengelyével párhuzamos, iránya az áram irányától és a tekercselés irányától függ, de a két esetben biztosan ellentétes.)
Az eredő mágneses indukció a tekercs és a körvezető áramának együttes hatására jön létre. A tekercs időben csökkenő mágneses indukciója a körvezetőben olyan feszültséget indukál, amelynek hatására meginduló áram a változást mérsékeli (Lenz-törvény), tehát \(\displaystyle B'\) a tekercs \(\displaystyle B\) indukcióját növeli. Az eredő mágneses indukció nagysága ezek szerint az \(\displaystyle a)\) alkérdésben szereplő időpont előtt \(\displaystyle \Delta t\) idővel
\(\displaystyle \vert B_1\vert =\vert B(-\Delta t)+B'\vert =\vert 0{,}13~{\rm mT}+0{,}05~{\rm mT}\vert =0{,}18~{\rm mT}, \)
utána pedig
\(\displaystyle \vert B_2\vert =\vert B(+\Delta t)+B'\vert =\vert -0{,}13~{\rm mT}+0{,}05~{\rm mT}\vert =0{,}08~{\rm mT}. \)
Statistics:
36 students sent a solution. 5 points: Bekes Nándor, Faisal Fahad AlSallom, Fajszi Bulcsú, Fehér 169 Szilveszter, Fekete Balázs Attila, Guba Zoltán, Iván Balázs, Kolontári Péter, Kovács 124 Marcell, Marozsák Tóbiás , Mocskonyi Mirkó, Nagy 555 Botond, Németh 123 Balázs, Németh 777 Róbert, Páhoki Tamás, Pécsi 117 Ildikó, Szentivánszki Soma , Tófalusi Ádám, Varga-Umbrich Eszter. 4 points: Di Giovanni András, Kondákor Márk, Magyar Róbert Attila, Pataki 245 Attila, Wesniczky Albert. 3 points: 10 students. 2 points: 2 students.
Problems in Physics of KöMaL, November 2016
