Problem P. 4881. (November 2016)

P. 4881. \(\displaystyle N\) converging lenses of focal length \(\displaystyle 2f\) and \(\displaystyle N\) diverging lenses of focal length \(\displaystyle -f\) are placed in turns onto an optical bench at a distance of \(\displaystyle f\) from each other. Then parallel to their common principal axis a beam of light of diameter \(\displaystyle D\) passes through the system of lenses

\(\displaystyle a)\) from the left;

\(\displaystyle b)\) from the right.

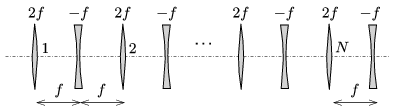
What is the light beam emerging from the system of lenses like?

(4 pont)

Deadline expired on December 12, 2016.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. \(\displaystyle a)\) Az optikai tengellyel párhuzamosan balról érkező fénysugarakat a gyüjtólencse \(\displaystyle 2f\) távolságban fókuszálná, ha nem lenne ott a szórólencse. Ez a pont a szórólencse jobb oldali fókuszpontja, tehát az oda tartó sugarakat párhuzamossá teszi, de ennek a nyalábnak az átmérője már csak \(\displaystyle D/2\). A további lencsepárokon áthaladó fénnyel ugyanez történik, így a lencserendszert párhuzamos, \(\displaystyle D/2^N\) átmérőjű nyaláb hagyja el.

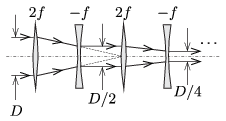
\(\displaystyle b)\) A jobbról érkező sugárnyalábbal hasonló történik, de a nyaláb mérete minden lencsepár után a 2-szeresére nő, így a végén \(\displaystyle 2^N\,D\) lesz. (Természetesen a nyaláb átmérőjének a lencsék mérete határt szab.)

Statistics:

40 students sent a solution.
4 points:	Berzsák Bulcsú, Bíró Dániel, Csuha Boglárka, Debreczeni Tibor, Elek Péter, Fehér 169 Szilveszter, Illés Gergely, Iván Balázs, Keltai Dóra, Kovács 124 Marcell, Krasznai Anna, Mácz Andrea, Makovsky Mihály, Markó Gábor, Marozsák Tóbiás , Mocskonyi Mirkó, Nagy 555 Botond, Németh 123 Balázs, Németh 777 Róbert, Nyerges Dóra, Olosz Adél, Ónodi Gergely, Póta Balázs, Pszota Máté, Szentivánszki Soma , Tibay Álmos, Tófalusi Ádám, Turcsányi Ádám, Vajay Mónika, Varga-Umbrich Eszter, Zsók Bianka.
3 points:	Illyés András, Murányi Albert, Simon Ákos.
2 points:	1 student.
1 point:	5 students.

Problems in Physics of KöMaL, November 2016