 Problem P. 4885. (December 2016)
Problem P. 4885. (December 2016)
P. 4885. Two boxes are placed onto each other as shown in the figure, and then they are released from the top of a slope of angle of elevation of \(\displaystyle \alpha\). The coefficient of static friction between the two boxes (of uniform density) is large enough so the two boxes do not slip on each other, but the two boxes slide together on the slope of coefficient of kinetic friction of \(\displaystyle \mu\).
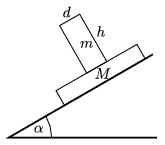
What is the condition for the box on the top not to be toppled over?
(5 pont)
Deadline expired on January 10, 2017.
Sorry, the solution is available only in Hungarian. Google translation
I. megoldás. A két doboz egyetlen testként \(\displaystyle a=g(\sin\alpha-\mu \cos\alpha)\) gyorsulással lefelé mozog a lejtőn. A \(\displaystyle m\) tömegű dobozra a függőlegesen lefelé mutató, \(\displaystyle mg\) nagyságú nehézségi erő, a lejtővel párhuzamos \(\displaystyle S\) súrlódási erő és a lejtőre merőleges \(\displaystyle N\) nyomóerő hat. A mozgásegyenletek (lejtő irányában és arra merőlegesen):
\(\displaystyle mg\sin\alpha-S=ma,\qquad mg\cos\alpha-N=0,\)
ahonnan a gyorsulás ismert értékét behelyettesítve
\(\displaystyle S=\mu mg\cos\alpha, \qquad N=mg\cos\alpha.\)
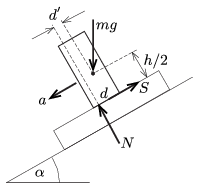
A felső doboz nem jön forgásba, emiatt a rá ható erők eredő forgatónyomatéka a tömegközéppontjára nézve nulla kell legyen:
\(\displaystyle N\,d'-S\,\frac{h}{2}=0, \qquad \text{azaz} \qquad \mu=\frac{2d'}{h}.\)
Mivel az \(\displaystyle N\) erő hatásvonala legfeljebb \(\displaystyle d/2\) távolságban lehet a felső doboz (tömeg)középpontjától (\(\displaystyle d'\le d/2\)), fenn kell álljon, hogy \(\displaystyle d\ge\mu h\).
II. megoldás. Írjuk fel a felső doboz egyensúlyának feltételét a dobozzal együtt mozgó koordináta-rendszerben. Ebben a gyorsuló rendszerben fellép egy \(\displaystyle ma=mg\sin\alpha-\mu mg\cos\alpha\) nagyságú, a lejtő mentén felfelé mutató tehetetlenségi erő, amelynek a támadáspontja (éppúgy, mint a nehézségi erőé) a test tömegközéppontja. Az eredő erő lejtő irányú komponense \(\displaystyle \mu mg\cos\alpha\), a lejtőre merőleges összetevő pedig \(\displaystyle mg\cos\alpha\). Az eredő erő hatásvonala akkor esik a két doboz érintkezési felületére (akkor nem billen fel a felső doboz), ha fennáll, hogy
\(\displaystyle \frac{\mu mg\cos\alpha}{ mg\cos\alpha}=\mu \le\frac{d}{h}.\)
Megjegyzés. Érdekes, hogy a fel nem borulás feltétele sem a dobozok tömegétől, sem a lejtő hajlásszögétől nem függ. Ha a súrlódás nagyon kicsi, akkor még egy nagyon ,,karcsú'' (\(\displaystyle d\ll h\)) doboz sem borul fel, miközben csúszik lefelé egy (akár nagyon meredek) lejtőn.
Statistics:
50 students sent a solution. 5 points: Bartók Imre, Bekes Nándor, Csire Roland, Csuha Boglárka, Elek Péter, Fehér 169 Szilveszter, Fekete Balázs Attila, Illés Gergely, Iván Balázs, Klučka Vivien, Köpenczei Csenge, Krasznai Anna, Marozsák Tóbiás , Molnár Mátyás, Morvai Orsolya, Németh 123 Balázs, Németh 777 Róbert, Olosz Adél, Ónodi Gergely, Páhoki Tamás, Pataki 245 Attila, Paulovics Péter, Sal Dávid, Szalay Gergő, Tófalusi Ádám, Tóth 111 Máté , Vígh Márton. 4 points: Kondákor Márk, Magyar Máté, Szentivánszki Soma , Varga-Umbrich Eszter. 3 points: 9 students. 2 points: 7 students. 1 point: 1 student. 0 point: 2 students.
Problems in Physics of KöMaL, December 2016
