Problem P. 4889. (December 2016)

P. 4889. A regular icosahedron is made of wires of the same length and of the same resistance of \(\displaystyle R\).

\(\displaystyle a)\) What is the equivalent resistance between two vertices which are opposite to each other?

\(\displaystyle b)\) What is the dissipated power at each resistor when a voltage of \(\displaystyle U\) is applied across these two opposite vertices?

(4 pont)

Deadline expired on January 10, 2017.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Az ikozaédernek 30 darab, egyenként \(\displaystyle R\) ellenállású oldaléle van. Az áram be- és kivezetési pontján átmenő tengely körüli \(\displaystyle 2\pi/5\) szögű forgatásokra nézve a kapcsolás szimmetrikus (ötfogású szimmetria). Az elforgatással egymásba vihető csúcspontok ekvipotenciálisak, így akár össze is köthetők.

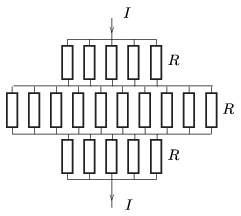
Az így kapott helyettesítő kapcsolás (amelyen az ekvipotenciális pontok közötti ellenállásokat nem tüntettük fel) eredő ellenállása már könnyen számolható:

\(\displaystyle R_\text{eredő}=R\left( \frac{1}{5}+ \frac{1}{10}+ \frac{1}{5}\right)= \frac 12 \, R.\)

\(\displaystyle b)\) \(\displaystyle U\) feszültség esetén az ikozaéderen keresztül összesen

\(\displaystyle I=\frac{U}{R_\text{eredő}}=\frac{2U}{R}\)

áram folyik. A be- és kivezetési ponthoz közeli \(\displaystyle 5+5\) ellenálláson \(\displaystyle \frac15I=\frac25\frac{U}{R}\) áram folyik, az egyes ellenállások teljesítménye: \(\displaystyle \frac{4}{25}\frac{U^2}{R}.\)

A középső ellenállásréteg 10 tagján egyenként \(\displaystyle \frac{1}{10}I\) áram folyik, és \(\displaystyle \frac{1}{25}\frac{U^2}{R}\) teljesítmény jut rájuk. Az ekvipotenciális pontok között lévő ellenállásokon nem folyik áram, tehát a rájuk eső teljesítmény nulla.

Statistics:

57 students sent a solution.
4 points:	Bekes Nándor, Csenger Géza, Elek Péter, Eper Miklós, Fehér 169 Szilveszter, Fekete Balázs Attila, Ghada Alshalan, Háder Márk István, Jánosik Áron, Klučka Vivien, Kolontári Péter, Kovács Gergely Balázs, Köpenczei Csenge, Krasznai Anna, Markó Gábor, Marozsák Tóbiás , Mocskonyi Mirkó, Nagy 555 Botond, Németh 123 Balázs, Németh 777 Róbert, Nguyen Viet Hung, Olosz Adél, Sal Dávid, Szakály Marcell, Szentivánszki Soma , Tófalusi Ádám, Tóth 420 Péter, Varga-Umbrich Eszter, Zöllner András, Zsombó István.
3 points:	Bíró Dániel, Faisal Fahad AlSallom, Fazakas Réka, Hajnal Dániel Konrád, Havasi Márton, Keltai Dóra, Magyar Róbert Attila, Nagy 284 Domonkos, Ónodi Gergely, Póta Balázs, Tóth Bence, Vajay Mónika.
2 points:	10 students.
1 point:	3 students.
0 point:	2 students.

Problems in Physics of KöMaL, December 2016