 Problem P. 4890. (December 2016)
Problem P. 4890. (December 2016)
P. 4890. A point-like object of mass \(\displaystyle m=1\) g and of charge \(\displaystyle Q=2\cdot 10^{-7}\) C is in uniform vertically upward electric field of magnitude \(\displaystyle E=6\cdot 10^4\) V/m. The object is given an initial downward speed of \(\displaystyle v_0=2\) m/s at an angle of \(\displaystyle \varphi=30^\circ\) with respect to the vertical.
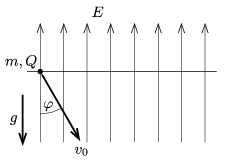
\(\displaystyle a)\) To what maximum depth measured from the level of projection does it go down?
\(\displaystyle b)\) How much time elapses until it reaches the lowest position?
\(\displaystyle c)\) What will its distance from its starting point be \(\displaystyle t=1.8\) s after it was started?
(5 pont)
Deadline expired on January 10, 2017.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. A testre függőlegesen felfelé \(\displaystyle QE-mg\) nagyságú erő hat, ez éppen akkora, mintha a nehézségi gyorsulás felfelé mutatna és
\(\displaystyle g'=\frac{QE}{m}-g=2{,}19~\frac{\rm m}{\rm s^2}\)
nagyságú lenne. Ebben a módosult ,,gravitációs térben'' a test a ferde hajítás törvényei szerint mozog.
\(\displaystyle a)\) A kezdősebesség függőleges komponense
\(\displaystyle v_1=v_0\,\cos\varphi=1{,}73~\frac{\rm m}{\rm s}.\)
A test legnagyobb lesüllyedése az indítás szintje alá:
\(\displaystyle h=\frac{v_1^2}{2g'}=0{,}6871~\rm m.\)
\(\displaystyle b)\) A pálya legmélyebb pontját
\(\displaystyle T=\frac{v_1}{g'}=0{,}79~\rm s\)
alatt éri el a test.
\(\displaystyle c)\) A megadott \(\displaystyle t\) idő alatt a test függőleges irányban \(\displaystyle y=\frac{g'}{2}t^2-v_1t= 0{,}43~\rm m\)-t, vízszintes irányban pedig (\(\displaystyle v_2=v_1\sin\varphi=1~\)m/s sebességű egyenletes mozgással) \(\displaystyle x=1{,}8~\)m-t mozdul el. A kiindulási ponttól való távolság ebben a pillanatban \(\displaystyle d=\sqrt{x^2+y^2}=1{,}85~\rm m\) lesz.
Statistics:
101 students sent a solution. 5 points: 64 students. 4 points: 22 students. 3 points: 7 students. 2 points: 1 student. 1 point: 3 students. 0 point: 1 student. Unfair, not evaluated: 3 solutionss.
Problems in Physics of KöMaL, December 2016
