 Problem P. 4893. (December 2016)
Problem P. 4893. (December 2016)
P. 4893. Bodies of different masses and different velocities are colliding with objects of mass \(\displaystyle M\), which are at rest. The collisions are head-on, totally elastic and the speed of each body is much less than the speed of light.
\(\displaystyle a)\) Determine the energy \(\displaystyle W\) given to the initially stationary object, in terms of the energy \(\displaystyle E\), and linear momentum \(\displaystyle I\) of the object which collides with it.
\(\displaystyle b)\) Sketch the graph of the function \(\displaystyle W(E,I)\) for fixed linear momentum \(\displaystyle I_0\), then for fixed energy \(\displaystyle E_0\).
\(\displaystyle c)\) Is it possible that an object having less energy gives more energy to the initially stationary body another one having more energy?
(6 pont)
Deadline expired on January 10, 2017.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. \(\displaystyle a)\) Ha a beeső test tömege \(\displaystyle m\), sebessége pedig \(\displaystyle v\), akkor a meglökött (\(\displaystyle M\) tömegű) test ütközés utáni sebessége (az energia- és az impulzusmegmaradás törvénye szerint)
\(\displaystyle V= \frac{2mM}{m+M}v,\)
mozgási energiája pedig
\(\displaystyle W=\frac{1}{2}M V^2=\frac{2m^2M}{(m+M)^2}v^2.\)
A \(\displaystyle v\) és \(\displaystyle m\) adatok kifejezhetők az ütköző részecske energiájával és impulzusával:
\(\displaystyle E=\frac{1}{2} mv^2, \qquad I=mv\)
alapján
\(\displaystyle m=\frac{I^2}{2E}, \qquad v=\frac{2E}{I},\)
ahonnan az átadott energia:
\(\displaystyle W(E,I)=8M\frac{I^2E^2}{(I^2+2ME)^2}.\)
Az energiaátadás ,,hatásfoka'':
\(\displaystyle \eta=\frac{W}{E}=8M\frac{I^2E}{(I^2+2ME)^2},\)
ami
\(\displaystyle \eta=\frac{mM}{\left(\frac{m+M}{2}\right)^2}\)
alakban is felírható. Nyilván \(\displaystyle \eta\le 1\), és az egyenlőség csak \(\displaystyle m=M\), vagyis \(\displaystyle I^2=2ME\) esetén teljesül.
\(\displaystyle b)\) Rögzített \(\displaystyle I_0\) impulzus esetén az átadott energia \(\displaystyle E\) függvényében az 1. ábrán látható, monoton növekvő görbével jellemezhető. Érdekes, hogy ha \(\displaystyle E\gg {I_0^2}/M\) (vagyis az ütköző test tömege nagyon kicsi, de a sebessége nagyon nagy), akkor az átadott energia véges nagyságú: \(\displaystyle W\approx 2I_0^2/M\).
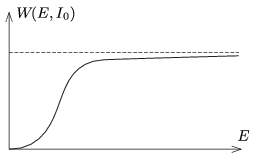
1. ábra
Rögzített \(\displaystyle E_0\) ,,bejövő energia'' esetén az átadott energia az \(\displaystyle I\) impulzus függvényében a 2. ábrán látható, maximummal rendelkező függvény. A maximum helye annak felel meg, hogy az ütköző test tömege \(\displaystyle m=M\), ekkor a teljes \(\displaystyle E=E_0\) energiáját átadja a kezdetben álló másik testnek.
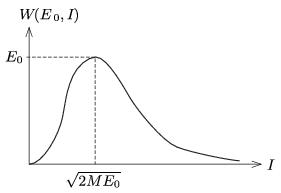
2. ábra
\(\displaystyle c)\) A 3. ábrán az átadott energiát \(\displaystyle I\) függvényében ábrázoltuk két különböző bejövő energia mellett (\(\displaystyle E_1<E_2\)).
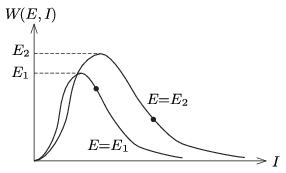
3. ábra
Látható, hogy egy kisebb energiájú test képes több energiát átadni egy adott tömegű álló testnek, mint egy nagyobb energiájú, amennyiben a bejövő részecskék impulzusa (avagy a tömege) lényegesen különböző.
Statistics:
38 students sent a solution. 6 points: Balaskó Dominik, Bartók Imre, Bekes Nándor, Csenger Géza, Csire Roland, Di Giovanni András, Édes Lili, Elek Péter, Fajszi Bulcsú, Fehér 169 Szilveszter, Fekete Balázs Attila, Hajnal Dániel Konrád, Iván Balázs, Kondákor Márk, Marozsák Tóbiás , Nagy 555 Botond, Németh 123 Balázs, Németh 777 Róbert, Olosz Adél, Páhoki Tamás, Póta Balázs, Pszota Máté, Sal Dávid, Szakály Marcell, Szentivánszki Soma , Tófalusi Ádám, Varga-Umbrich Eszter. 5 points: Bukor Benedek, Faisal Fahad AlSallom, Jakus Balázs István, Molnár Mátyás, Morvai Orsolya, Németh Csaba Tibor, Osváth Botond. 4 points: 2 students. 1 point: 1 student. 0 point: 1 student.
Problems in Physics of KöMaL, December 2016
