 Problem P. 4896. (January 2017)
Problem P. 4896. (January 2017)
P. 4896. A small sport plane makes a trip, first flying into a headwind, from \(\displaystyle A\) to \(\displaystyle B\) towards the north in 3 hours, whilst the backward trip from \(\displaystyle B\) to \(\displaystyle A\) flying with tailwind takes 2 hours. How long would the full trip (i.e., forth and back) take if the wind blew constantly from the northeast? (The speed of the wind can be considered as constant.)
(4 pont)
Deadline expired on February 10, 2017.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Jelöljük a szélsebesség vektorát \(\displaystyle \boldsymbol c\)-vel, repülő sebességét a levegőhöz képest \(\displaystyle \boldsymbol v\)-vel, az elmozdulásvektort pedig \(\displaystyle \boldsymbol d\)-vel. A szél iránya zárjon be \(\displaystyle \alpha\) szöget az észak-déli iránnyal! (Szembeszélnél \(\displaystyle \alpha=180^\circ\), hátszélnél \(\displaystyle \alpha=0\), északkeleti szélben pedig odafelé \(\displaystyle 135^\circ\), visszafelé \(\displaystyle 45^\circ\).
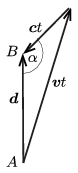
A repülőút \(\displaystyle t\) idejét az ábrán látható vektorháromszögből kaphatjuk meg, ha alkalmazzuk a koszinusztételt.
\(\displaystyle v^2t^2=c^2t^2+d^2-2dct\cos\alpha,\)
ahonnan a számunkra értelmes megoldás:
\(\displaystyle t=d\frac{\sqrt{v^2-c^2\sin\alpha}-c\cos\alpha}{v^2-c^2}.\)
A szembeszélnek és a hátszélnek megfelelő adatokból
\(\displaystyle 3~\text{óra}=\frac{d}{v-c},\)
\(\displaystyle 2~\text{óra}=\frac{d}{v+c},\)
amiből \(\displaystyle v=5\,c\) és \(\displaystyle d=v\cdot 2{,}4~\)óra következik. (Látható, hogy szélcsendes időben a repülőgép 2,4 óra alatt érne az egyik helytől a másikig.
Más szélirány esetén a repülési idő (órában kifejezve):
\(\displaystyle t=\frac{\sqrt{25-\sin^2\alpha}-\cos\alpha}{2},\)
innen az \(\displaystyle 135^\circ\)-hoz és \(\displaystyle 45^\circ\)-hoz tartozó repülési idők: 2,83 óra és 2,12 óra.
Északkeleti szélben tehát összesen 4,95 óra hosszú a repülési idő, ez csak nagyon kicsit tér el az északi szélben történő oda-vissza repülés teljes idejétől.
Statistics:
83 students sent a solution. 4 points: Ardai István Tamás, Balaskó Dominik, Bartók Imre, Boros Máté, Bukor Benedek, Conrád Márk, Csuha Boglárka, Édes Lili, Faisal Fahad AlSallom, Fajszi Bulcsú, Fazakas Réka, Fehér 169 Szilveszter, Gál Péter Levente, Guba Zoltán, Háder Márk István, Illés Gergely, Illyés András, Jánosik Áron, Kavas Katalin, Keltai Dóra, Klučka Vivien, Kovács 526 Tamás, Krasznai Anna, Kürti Zoltán, Mamuzsics Gergő Bence, Merkl Gergely, Molnár 957 Barnabás, Molnár Mátyás, Morvai Orsolya, Murányi Albert, Németh Csaba Tibor, Olosz Adél, Ónodi Gergely, Páhoki Tamás, Papp 121 Krisztina, Póta Balázs, Pszota Máté, Sal Dávid, Soós Benjámin, Tibay Álmos, Tófalusi Ádám, Tóth Bence, Veres Károly, Weisz Máté. 3 points: 7 students. 2 points: 1 student. 1 point: 27 students. 0 point: 4 students.
Problems in Physics of KöMaL, January 2017
