 Problem P. 4900. (January 2017)
Problem P. 4900. (January 2017)
P. 4900. An interesting optical toy consists of two opposite concave spherical mirrors, having the same radius of curvature, the one at the top having a circular hole of diameter of a few centimetres at its centre. The distance between the mirrors is set in a way, that if a small object (e.g. a piece of candy) is placed at the centre of the mirror at the bottom, then its image is formed at the centre of the mirror with the hole in it. The light beam forms the image after a reflection first in the top, then in the bottom mirror.
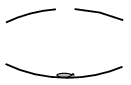
\(\displaystyle a)\) What is the distance between the centers of the two mirrors?
\(\displaystyle b)\) Is the image upright or inverted? Is it a virtual or a real image? What is the magnification?
(5 pont)
Deadline expired on February 10, 2017.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. \(\displaystyle a)\) Jelöljük a tükrök fókusztávolságát \(\displaystyle f\)-fel, az optikai tengely mentén mért távolságukat pedig \(\displaystyle d\)-vel. A felső tükör a \(\displaystyle t_1=d\) távol lévő tárgyról a leképezési törvény szerint
\(\displaystyle k_1=\frac{df}{d-f}\)
távolságban alkot (valódi vagy látszólagos) képet. Ez a kép az alsó tükörtől
\(\displaystyle t_2=d-k_1=\frac{d(d-2f)}{d-f}\)
távol lévő tárgynak tekinthető, amelynek a képe (az alsó tükör felett)
\(\displaystyle k_2=\frac{t_2f}{t_2-f}=\frac{fd(d-2f)}{d^2-3fd+f^2}\)
magasságban képződik. A megadott feltétel szerint \(\displaystyle k_2=d\), tehát
\(\displaystyle \frac{fd(d-2f)}{d^2-3fd+f^2}=d,\)
vagyis
\(\displaystyle d^2-4df+3f^2=0.\)
Ennek a másodfokú egyenletnek 2 valós gyöke van:
\(\displaystyle d_1=f=\frac12R \qquad \text{és} \qquad d_2=3f=\frac32R.\)
\(\displaystyle b)\) A nagyítás
\(\displaystyle N=\frac{k_1}{t_1}\frac{k_2}{t_2}=\frac{f^2}{d^2-3fd+f^2}.\)
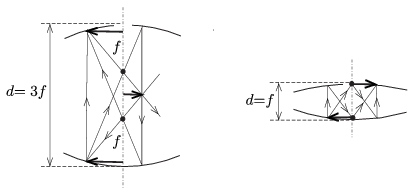
Ha \(\displaystyle d=d_1=f\), akkor a nagyítás \(\displaystyle -1\), tehát a kép fordított állású, ha pedig \(\displaystyle d=d_2=3f\), akkor a nagyítás \(\displaystyle +1\), tehát a kép egyenes állású. Mindkét esetben a kép valódi, vagyis ernyővel felfogható, de – megfelelő irányból nézve – szabad szemmel is látható. A képalkotás néhány nevezetes sugármenet segítségével könnyen megszerkeszthető.
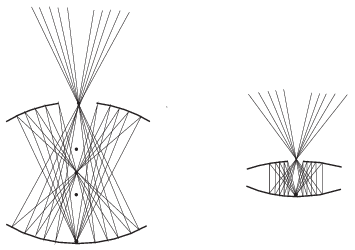
A szerkesztésnél használt segédvonalak nem mindegyike felel meg tényleges fénysugárnak, hiszen a felső tükör közepén egy lyuk van. Az alábbi ábrán a tárgy egy (az egyszerűség kedvéért az optikai tengelyen fekvő) pontjából kiinduló fénysugarakat ábrázoltuk a tükrök kétféle beállítása mellett. Látható, hogy az optikai tengely közelében van egy olyan tartomány, ahonnan nézve nem láthatjuk a lyuk közepén keletkező valódi képet (hanem csak az alsó tükör közepén lévő tárgyat). A furcsa, fent lebegni látszó képet csak kicsit ,,oldalról'' figyelhetjük meg.
Statistics:
24 students sent a solution. 5 points: Fajszi Bulcsú, Fehér 169 Szilveszter, Fekete Balázs Attila, Marozsák Tóbiás , Nagy 555 Botond, Németh 123 Balázs, Németh 777 Róbert, Olosz Adél, Páhoki Tamás, Paulovics Péter, Szentivánszki Soma , Tóth 111 Máté . 4 points: Bekes Nándor, Molnár Mátyás, Varga-Umbrich Eszter. 3 points: 7 students. 2 points: 2 students.
Problems in Physics of KöMaL, January 2017
