 Problem P. 4903. (January 2017)
Problem P. 4903. (January 2017)
P. 4903. A small ball of mass \(\displaystyle m\) and of charge \(\displaystyle Q\) is attached to the bottom end of a piece of negligible-mass thread of length \(\displaystyle L\), whose top end is fixed. The system formed by the thread and the ball is in uniform magnetic field, \(\displaystyle \boldsymbol B\), which is perpendicular to the plane of the figure and points into the paper.
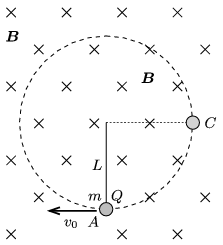
The ball is started in a direction perpendicular both to the magnetic induction and to the direction of the thread. At a certain initial speed the ball moves along a circular path such that the thread remains tight during the whole motion.
\(\displaystyle a)\) What is the magnitude of the magnetic induction \(\displaystyle B\) if the minimum initial speed at which the described motion of the ball occurs is \(\displaystyle v_0=\frac 12 \sqrt{17Lg}\,\)?
\(\displaystyle b)\) By what factor is the force acting on the thread at point \(\displaystyle A\) greater than that at point \(\displaystyle C\), when the initial speed of the ball is the above stated one?
(5 pont)
Deadline expired on February 10, 2017.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. A mágneses Lorentz-erő merőleges a test sebességére (így nem végez munkát), iránya \(\displaystyle Q>0\) és a megadott irányú mágneses indukció és sebesség esetén ,,kifelé'' mutat. Amikor a fonál \(\displaystyle \alpha\) szöget zár be a függőlegessel, a golyó sebessége (az energiamegmaradás törvénye szerint)
\(\displaystyle v=\sqrt{v_0^2-2Lg(1-\cos\alpha)},\)
éppen ugyanakkora, mint amekkora mágneses tér nélküli esetben lenne. A megadott nagyságú \(\displaystyle v_0\) mellett a sebesség így is felírható:
\(\displaystyle v(\alpha)=\frac{3}{2}\sqrt{Lg}\sqrt{1+\frac{8}{9}\cos\alpha}.\)
A test mozgásegyenlete (pontosabban annak sugár irányú komponense) az ábrán látható helyzetben:
\(\displaystyle K-mg\cos\alpha-QvB=\frac{mv^2}{L},\)
amibe \(\displaystyle v(\alpha)\) fentebb kiszámított kifejezését beírva a fonalat feszítő erőre a
\(\displaystyle K(\alpha)=mg\left( 3\cos\alpha+\frac{9}{4}+\frac{QB}{2mg}\sqrt{Lg(9+8\cos\alpha)}\right) \)
kifejezést kapjuk. Ez a függvény a \(\displaystyle 0<\alpha<180^\circ\) intervallumban monoton csökken, tehát ha még a pálya tetőpontján \(\displaystyle \alpha=180^\circ\)-nál sem válik negatívvá, akkor a körpálya más részén sem lazulhat meg a fonál.
\(\displaystyle a)\) Mivel \(\displaystyle v_0\) megadott értéke az a legkisebb kezdősebesség, amellyel indítva a testet a fonál még éppen nem lazul meg sehol, ebben a határesetben \(\displaystyle K(180^\circ)=0\) teljesül. Eszerint a mágneses indukció nagysága
\(\displaystyle B=\frac{3}{2}\,\frac{mg}{Q\sqrt{Lg}},\)
és a fonalat feszítő erő tetszőleges helyzetben
\(\displaystyle K(\alpha)=mg\left( 3\cos\alpha+\frac{9}{4}+\frac{3}{4}\sqrt{9+8\cos\alpha}\right). \)
\(\displaystyle b)\) A fonálerő a \(\displaystyle C\) pontban (\(\displaystyle \alpha=0\) esetén)
\(\displaystyle K_A=\frac{21+3\sqrt{17}}{4}mg\approx 8{,}3\,mg,\)
a \(\displaystyle C\) pontban (\(\displaystyle \alpha=90^\circ\)-os szögnél) pedig
\(\displaystyle K_C=\frac{9}{2}\,mg=4{,}5\,mg,\)
a kérdezett arány tahát
\(\displaystyle \frac{K_A}{K_C}=\frac{21+3\sqrt{17}}{18}\approx 1{,}8.\)
Statistics:
54 students sent a solution. 5 points: Csuha Boglárka, Di Giovanni András, Faisal Fahad AlSallom, Fekete Balázs Attila, Ghada Alshalan, Illés Gergely, Jakus Balázs István, Kolontári Péter, Krasznai Anna, Makovsky Mihály, Marozsák Tóbiás , Németh 123 Balázs, Zöllner András. 4 points: Bartók Imre, Bekes Nándor, Bukor Benedek, Csire Roland, Elek Péter, Eper Miklós, Fajszi Bulcsú, Fehér 169 Szilveszter, Guba Zoltán, Illyés András, Kondákor Márk, Kormányos Hanna Rebeka, Magyar Róbert Attila, Molnár Mátyás, Nagy 555 Botond, Németh 777 Róbert, Németh Csaba Tibor, Olosz Adél, Páhoki Tamás, Papp 121 Krisztina, Pataki 245 Attila, Sugár Soma, Szentivánszki Soma , Tófalusi Ádám, Tóth 111 Máté . 3 points: 7 students. 2 points: 4 students. 1 point: 3 students. 0 point: 2 students.
Problems in Physics of KöMaL, January 2017
