 Problem P. 4904. (January 2017)
Problem P. 4904. (January 2017)
P. 4904. The initial voltage across the capacitor of capacitance \(\displaystyle C\), connected as shown in the figure is \(\displaystyle 2U_0\), whilst the capacitor of capacitance \(\displaystyle 2C\) is neutral.
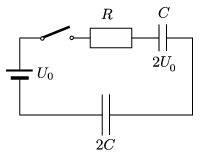
How much heat is dissipated at the resistor of resistance \(\displaystyle R\) after closing the switch?
(6 pont)
Deadline expired on February 10, 2017.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. A kapcsoló zárása után az ellenálláson (időben változó nagyságú) áram folyik keresztül, ennek az áramnak a hőhatására vagyunk kiváncsiak. A Joule-hő például az időben változó \(\displaystyle P=I^2R\) teljesítmény integrálásával határozható meg, de elemi úton, az energiaviszonyok megvizsgálásával is kiszámítható.
Tudjuk, hogy a \(\displaystyle C\) kapacitású kondenzátor feszültségének nagysága \(\displaystyle 2U_0\), de a feszültség előjele nem derül ki a feladat szövegéből. Emiatt meg kell vizsgálnunk mindkét polaritás lehetőségét.
\(\displaystyle a)\) Legyen a \(\displaystyle C\) kapacitású (a rajzon felső) kondenzátor jobb oldali lemeze kezdetben \(\displaystyle +2CU_0\) töltésű, a bal oldali lemez töltése ennek \(\displaystyle (-1)\)-szerese. A másik (alsó) kondenzátor töltetlen. A kapcsoló zárása után a felső kondenzátor átad valamekkora \(\displaystyle \Delta Q\) töltést az alsó kondenzátornak, így a töltésük \(\displaystyle 2CU_0-\Delta Q\), illetve \(\displaystyle \Delta Q\) lesz. Kirchhoff II. törvénye szerint az áramkörben a körfeszültség nulla:
\(\displaystyle U_0+\frac{2CU_0-\Delta Q}{C}-\frac{\Delta Q}{2C}=0,\)
ahonnan kiszámítható az átadott töltés:
\(\displaystyle \Delta Q=2CU_0.\)
Ugyanekkora töltés kerül a felső kondenzátor bal oldali lemezére, ezt a telep adja le. Végeredményben a felső kondenzátor elveszíti az összes töltését, az alsó pedig \(\displaystyle 2CU_0\) töltéssel feltöltődik.
A két kondenzátor elektrosztatikus összenergiája kezdetben
\(\displaystyle {\cal E}_1=\frac{1}{2}\frac{(2CU_0)^2}{C}+0=2CU_0^2\)
volt. A kapcsoló zárása után kialakult helyzetben a kondenzátorok összenergiája:
\(\displaystyle {\cal E}_2=0+\frac{1}{2}\frac{(2CU_0)^2}{2C}=CU_0^2.\)
Az elektrosztatikus energia megváltozása:
\(\displaystyle \Delta {\cal E}_\text{kondenzátor}={\cal E}_2-{\cal E}_1= -CU_0^2.\)
Ne feledkezzünk meg arról sem, hogy a két kondenzátor csak a teleppel együtt alkot zárt rendszert, és a folyamat során a telep energiája is megváltozik, hiszen lead \(\displaystyle \Delta Q\) töltést:
\(\displaystyle \Delta {\cal E}_\text{telep}=-U_0\Delta Q=-2CU_0^2.\)
A rendszer teljes energiájának csökkenése az ellenálláson fejlődő \(\displaystyle W\) hővel egyenlő:
\(\displaystyle W=-\Delta {\cal E}_\text{kondenzátor}-\Delta {\cal E}_\text{telep}=+3CU_0^2.\)
\(\displaystyle b)\) Hasonló módon számolhatjuk ki a másik polaritással feltöltött kondenzátor esetét is. Ha a felső kondenzátor jobb oldali lemezén kezdetben \(\displaystyle -2CU_0\) töltés van, a kapcsoló zárása után eltávozik róla \(\displaystyle \Delta Q\) töltés, akkor a huroktörvény szerint
\(\displaystyle U_0+\frac{-2CU_0-\Delta Q}{C}-\frac{\Delta Q}{2C}=0.\)
Innen következik, hogy
\(\displaystyle \Delta Q=-\frac{2}{3}CU_0,\)
a felső kondenzátor jobb oldali lemezének töltése tehát \(\displaystyle -\frac{4}{3}CU_0\)-ra, az alsó kondenzátor töltése pedig \(\displaystyle \pm \frac{2}{3}CU_0\)-ra változik.
Az energiaviszonyok változása most így alakul:
\(\displaystyle \Delta {\cal E}_\text{kondenzátor}={\cal E}_2-{\cal E}_1= \frac12 \left(\frac{16}{9}+\frac{4}{9}\frac{1}{2}-4\right)CU_0^2=-CU_0^2,\)
vagyis ugyanannyi, mint az előző esetben, de a telep energiaváltozása
\(\displaystyle \Delta {\cal E}_\text{telep}=-U_0\Delta Q=\frac23CU_0^2.\)
(A telep most felvesz töltéseket, emiatt az energiája növekszik.)
A fejlődő hő ebben az esetben
\(\displaystyle W=-\Delta {\cal E}_\text{kondenzátor}-\Delta {\cal E}_\text{telep}=+\frac13CU_0^2.\)
Megjegyzés. Belátható, hogy ha egy ellenálláson időben exponenciálisan csökkenő áram folyik keresztül (esetünkben éppen ez történik), akkor a kisülési folyamat során fejlődő teljes Joule-hő az ellenállásra eső kezdeti (maximális) feszültség és az ellenálláson átfolyó töltés szorzatának felével egyezik meg. A feladatban szereplő kapcsolásnál ez
\(\displaystyle \tfrac12 (3U_0)(2CU_0)=3CU_0^2,\qquad \text{illetve}\qquad \tfrac12 (-U_0)(-\tfrac23CU_0)=\tfrac13CU_0^2.\)
Statistics:
26 students sent a solution. 6 points: Elek Péter, Fehér 169 Szilveszter, Fekete Balázs Attila, Jakus Balázs István, Marozsák Tóbiás , Nagy 555 Botond, Németh 777 Róbert, Olosz Adél, Sal Dávid, Szentivánszki Soma . 5 points: Bekes Nándor, Kolontári Péter, Németh 123 Balázs, Tófalusi Ádám. 4 points: 5 students. 3 points: 3 students. 2 points: 2 students. 1 point: 1 student. 0 point: 1 student.
Problems in Physics of KöMaL, January 2017
