 Problem P. 4916. (March 2017)
Problem P. 4916. (March 2017)
P. 4916. There is a slope of height \(\displaystyle H\) and of elevation angle of \(\displaystyle \alpha\) at rest on the level ground. There is a small point-like object next to the slope. At what acceleration must the slope be moved in order that the point-like object reaches its top in a time of \(\displaystyle t\)? (Friction is negligible.)
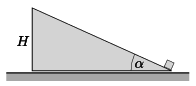
Data: \(\displaystyle \alpha=30^\circ\), \(\displaystyle H=0.2\) m, \(\displaystyle t=0.2\) s.
(4 pont)
Deadline expired on April 10, 2017.
Sorry, the solution is available only in Hungarian. Google translation
I. megoldás. Jelöljük a lejtő gyorsulását (jobbra) \(\displaystyle a_0\)-lal, a pontszerű test függőleges gyorsulását \(\displaystyle a_1\)-gyel, vízszintes gyorsulását pedig (ugyancsak jobbra) \(\displaystyle a_2\)-vel. (Mindezek a gyorsulások a talajhoz képest értendők.)
A megadott feltételek szerint
| \(\displaystyle (1)\) | \(\displaystyle \frac{a_1}{2}t^2=H,\) |
| \(\displaystyle (2)\) | \(\displaystyle \frac{a_2}{2}t^2=\frac{a_0}{2}t^2-\frac{H}{\tg\alpha}.\) |
Ha a lejtő \(\displaystyle N\) nagyságú erőt fejt ki a kis testre, a mozgásegyenletek:
| \(\displaystyle (3)\) | \(\displaystyle N\cos\alpha-mg=ma_1,\) |
| \(\displaystyle (4)\) | \(\displaystyle N\sin\alpha=ma_2.\) |
A fenti egyenletekből \(\displaystyle a_1, a_2\) és \(\displaystyle N\) kiküszöbölése után a lejtő gyorsulására
\(\displaystyle a_0=g\tg\alpha+\frac{2H}{t^2\sin\alpha\,\cos\alpha}=28{,}8~\frac{\rm m}{\rm s^2}\)
adódik.
II. megoldás. Írjuk le a pontszerű test mozgását a lejtőhöz rögzített koordináta-rendszerben! Ebben a gyorsuló vonatkoztatási rendszerben a testre ható, függőlegesen lefelé irányuló, \(\displaystyle mg\) nagyságú nehézségi erő mellett fellép egy vízszintesen balra mutató, \(\displaystyle ma_0\) nagyságú tehetetlenségi erő is. Az eredő erő hatására a test
\(\displaystyle A=a_0\cos\alpha-g\sin\alpha\)
gyorsulással mozog a lejtőn felfelé, és az
\(\displaystyle s=\frac{H}{\sin\alpha}\)
hosszúságú utat a megadott \(\displaystyle t\) idő alatt teszi meg, tehát
\(\displaystyle \frac{a_0\cos\alpha-g\sin\alpha}{2}t^2=\frac{H}{\sin\alpha}.\)
Innen
\(\displaystyle a_0=g\tg\alpha+\frac{2H}{t^2\sin\alpha\,\cos\alpha}=28{,}8~\frac{\rm m}{\rm s^2}. \)
Statistics:
65 students sent a solution. 4 points: Augusztin András Balázs, Balaskó Dominik, Balog 518 Lóránd, Bartók Imre, Bíró Dániel, Bukor Benedek, Csuha Boglárka, Édes Lili, Fajszi Bulcsú, Fazakas Réka, Fehér 169 Szilveszter, Fekete Balázs Attila, Gál Péter Levente, Guba Zoltán, Hajdu 046 Ákos, Illés Gergely, Jánosik Áron, Keltai Dóra, Klučka Vivien, Kondákor Márk, Kovács Gergely Balázs, Kozák András, Köpenczei Csenge, Krasznai Anna, Krizsán László, Kürti Zoltán, Magyar Róbert Attila, Makai Enikő, Mamuzsics Gergő Bence, Markó Gábor, Marozsák Tóbiás , Merkl Gergely, Molnár 957 Barnabás, Molnár Mátyás, Nagy 555 Botond, Németh 123 Balázs, Németh Csaba Tibor, Nenezic Patrick Uros, Olosz Adél, Páhoki Tamás, Pataki 245 Attila, Paulovics Péter, Póta Balázs, Richlik Róbert, Sal Dávid, Takács Attila, Tófalusi Ádám, Tóth 111 Máté , Zeke Norbert. 3 points: 7 students. 2 points: 2 students. 1 point: 4 students. 0 point: 3 students.
Problems in Physics of KöMaL, March 2017
