 Problem P. 4919. (March 2017)
Problem P. 4919. (March 2017)
P. 4919. A trolley of mass \(\displaystyle m_1\) was placed to a horizontal, rigid pair of rails at some height as shown in the figure. There is a small ball of mass \(\displaystyle m_2\) attached to one end of a thread, whose other end is attached to the bottom of the trolley. (The thread hangs between the rails. The length of the thread is much greater than the size of the ball and the trolley.)
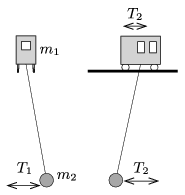
If the ball is displaced a bit from its stable equilibrium position in the direction perpendicular to the rails, then it swings with a period of \(\displaystyle T_1\). If the ball is displaced a bit parallel to the rails, while the trolley is fixed, and then both the ball and the trolley are released, then the period of the oscillation is \(\displaystyle T_2\). What is the ratio of \(\displaystyle m_2/m_1\), if \(\displaystyle T_1/T_2=2\)? (Friction and air drag are negligible.)
(5 pont)
Deadline expired on April 10, 2017.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. A sínekre merőlegesen kitérített golyó (mint matematikai inga)
\(\displaystyle T_1=2\pi\sqrt{\frac{\ell}{g}}\)
lengésidővel mozog.
A sínekkel (jó közelítéssel) párhuzamos mozgás során a kiskocsi és a golyó tömegközéppontja vízszintes irányban nem mozdul el, a függőleges elmozdulása pedig (kis kitérések esetén) másodrendűen kicsi, elhanyagolható. A fonalat feszítő erő \(\displaystyle m_2g\), hiszen a golyó függőleges irányú elmozdulása (és így a gyorsulása is) elhanyagolhatóan kicsi. Ha a kiskocsi elmozdulása \(\displaystyle x\), a sínek alatt \(\displaystyle h=\ell\frac{m_2}{m_1+m_2}\) mélyen lévő tömegközépponton áthaladó fonál a kiskocsira
\(\displaystyle F=-m_2g\frac{x}{h}=-\left(m_1+m_2\right) \frac{g}{\ell}\, x\)
vízszintes irányú erőt fejt ki, ami a harmonikus rezgőmozgást végző test mozgásegyenlete szerint \(\displaystyle -m_1x\omega_2^2\)-tel egyenlő. Innen következik, hogy a lengésidő ebben az esetben
\(\displaystyle T_2=\frac{2\pi}{\omega_2}=2\pi \sqrt{\frac{\ell}{g}\, \frac{m_1}{m_1+m_2}}=T_1\sqrt{\frac{m_1}{m_1+m_2}}.\)
(Ugyanezt az eredményt kapjuk, ha a golyó vízszintes irányú mozgásegyenletét írjuk fel.)
A megadott \(\displaystyle T_1/T_2=2\) feltétel akkor teljesül, ha \(\displaystyle m_2/m_1=3.\)
Statistics:
32 students sent a solution. 5 points: Bartók Imre, Bekes Nándor, Csire Roland, Csuha Boglárka, Debreczeni Tibor, Di Giovanni András, Elek Péter, Fehér 169 Szilveszter, Fekete Balázs Attila, Illés Gergely, Jánosik Áron, Krasznai Anna, Markó Gábor, Marozsák Tóbiás , Nagy 555 Botond, Németh 123 Balázs, Németh 777 Róbert, Olosz Adél, Ónodi Gergely, Páhoki Tamás, Póta Balázs, Sal Dávid, Szentivánszki Soma , Tófalusi Ádám, Varga-Umbrich Eszter, Zöllner András. 4 points: Papp 121 Krisztina. 3 points: 1 student. 2 points: 2 students. 1 point: 2 students.
Problems in Physics of KöMaL, March 2017
