 Problem P. 4928. (April 2017)
Problem P. 4928. (April 2017)
P. 4928. \(\displaystyle a)\) At what accelerations do the trolleys shown in the figure start to move if the wheels can roll easily, and the mass of the pulley and air drag are negligible? Data: \(\displaystyle m_1=1\) kg, \(\displaystyle m_2=2\) kg, \(\displaystyle M=5\) kg.
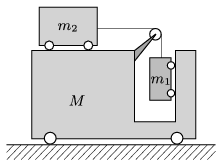
\(\displaystyle b)\) For other mass values, in what interval can the value of the initial acceleration of the trolley of mass \(\displaystyle M\) be?
(5 pont)
Deadline expired on May 10, 2017.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Jelöljük a testekre ható erőket és a testek gyorsulását az ábrán látható módon! (Az \(\displaystyle m_2\) tömegű kiskocsi a \(\displaystyle M\) tömegű kocsikoz képest \(\displaystyle a\), a talajhoz képest tehát \(\displaystyle a-A\) gyorsulással mozog.)
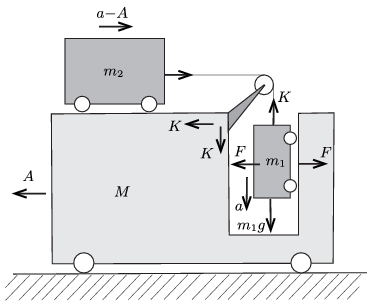
A mozgásegyenletek:
\(\displaystyle m_1g-K=m_1a,\)
\(\displaystyle K-F=MA,\)
\(\displaystyle K=m_2(a-A),\)
\(\displaystyle F=m_1A.\)
Az egyenletrendszer megoldása:
\(\displaystyle A=\frac{m_1m_2}{m_1\left(m_1+m_2+M\right)+m_2\left(m_1+M\right) }\,g,\)
\(\displaystyle a=\frac{m_1\left(m_1+m_2+M\right) }{m_1\left(m_1+m_2+M\right)+m_2\left(m_1+M\right) }\,g.\)
\(\displaystyle a)\) A megadott tömegek esetén
\(\displaystyle A=\frac{1}{10}g=0{,}98~\frac{\rm m}{\rm s^2}\approx 1{,}0 ~\frac{\rm m}{\rm s^2},\)
\(\displaystyle a=\frac{2}{5}g=3{,}92~\frac{\rm m}{\rm s^2}\approx 4{,}0 ~\frac{\rm m}{\rm s^2},\)
\(\displaystyle a-A=\frac{3}{10}g=2{,}94~\frac{\rm m}{\rm s^2}\approx 3{,}0 ~\frac{\rm m}{\rm s^2}.\)
\(\displaystyle b)\) Az \(\displaystyle M\) tömegű kiskocsi gyorsulása így is felírható:
\(\displaystyle A=\frac{g}{2+\frac{m_1}{m_2}+\frac{M}{m_1}+\frac{M}{m_2}}.\)
Látható, hogy
\(\displaystyle 0<A<\frac{g}{2} .\)
Az \(\displaystyle A\approx \tfrac12 g\) felső korlát akkor közelíthető meg, ha \(\displaystyle M\ll m_1 \ll m_2\). Ebben a határesetben \(\displaystyle F\approx K\approx \frac{1}{2}m_2g\) és \(\displaystyle a\approx A\).
Statistics:
39 students sent a solution. 5 points: Bekes Nándor, Fehér 169 Szilveszter, Fekete Balázs Attila, Magyar Róbert Attila, Mamuzsics Gergő Bence, Marozsák Tóbiás , Németh 123 Balázs, Németh 777 Róbert, Olosz Adél, Páhoki Tamás, Pécsi 117 Ildikó, Póta Balázs, Sal Dávid, Varga-Umbrich Eszter. 4 points: Berke Martin, Illés Gergely. 3 points: 1 student. 2 points: 1 student. 1 point: 19 students. 0 point: 2 students.
Problems in Physics of KöMaL, April 2017
