 |
A P. 4929. feladat (2017. április) |
P. 4929. Az ábrán látható, \(\displaystyle 3L\) hosszúságú, elhanyagolható tömegű, merev rúd a bal oldali végétől \(\displaystyle L\) távolságra lévő, rögzített, vízszintes tengely körül függőleges síkban súrlódásmentesen foroghat. A rúd végeihez \(\displaystyle m\), illetve \(\displaystyle 2m\) tömegű, kis méretű testeket erősítünk, majd egy adott pillanatban a rudat vízszintes helyzetből elengedjük.
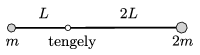
\(\displaystyle a)\) Határozzuk meg a testek sebességét abban a pillanatban, amikor a rúd éppen függőleges!
\(\displaystyle b)\) Mekkora erővel nyomja ekkor a rúd a tengelyt?
\(\displaystyle c)\) Mekkora a testek gyorsulása a rúd elengedése utáni pillanatban?
Közli: Kotek László, Pécs
(4 pont)
A beküldési határidő 2017. május 10-én LEJÁRT.
Megoldás. \(\displaystyle a)\) Ha az éppen függőleges rúd szögsebességét \(\displaystyle \omega\)-val jelöljük, akkor az \(\displaystyle m\) tömegű test sebessége \(\displaystyle v_1=L\omega\), a \(\displaystyle 2m\) tömegű másik testé pedig \(\displaystyle v_2=2L\omega\) lesz. Az energiamegmaradás tétele szerint
\(\displaystyle \frac{1}{2}m L^2\omega^2+\frac{1}{2}(2m) (2L)^2\omega^2=(2mg)(2L)-mgL,\)
és innen
\(\displaystyle \omega=\sqrt{\frac{2g}{3L}} ,\qquad v_1=\sqrt{\frac{2}{3}Lg} ,\qquad v_2=\sqrt{\frac{8}{3}Lg}.\)
\(\displaystyle b)\) A Newton-egyenlet szerint a rúd által az egyes testekre kifejtett függőlegesen felfelé irányuló erő:
\(\displaystyle F_1=mg-mL\omega^2=\frac13mg,\)
\(\displaystyle F_2=(2m)g+(2m)(2L)\omega^2=\frac{14}3mg,\)
ezek ellenerejével, tehát összesen \(\displaystyle 5mg\) nagyságú erővel hat a két test a rúdra lefelé. Mivel a rúd tömege elhanyagolható, ugyancsak \(\displaystyle 5mg\) nagyságú, de függőlegesen felfelé mutató erővel hat a tengely a rúdra. Ezek szerint a rúd a tengelyt \(\displaystyle 5mg\) nagyságú erővel nyomja lefelé.
\(\displaystyle c)\) Az indulás pillanatában az \(\displaystyle m\) tömegú test valamekkora \(\displaystyle a\) gyorsulással indul el felfelé, a \(\displaystyle 2m\) tömegű test pedig \(\displaystyle 2a\) gyorsulással lefelé. A rúd az indulás pillanatában olyan két erővel hat a két testre, amelyek ellenerejének forgatónyomatéka a tengelyre nulla. (Ha nem így lenne, akkor az elhanyagolható tömegű rúd nagyon nagy szöggyorsulással indulna el.) Ha a rúd a bal oldali testre \(\displaystyle 2F\), a jobb oldali testre \(\displaystyle F\) erőt fejt ki felfelé, akkor a mozgásegyenletek:
\(\displaystyle 2F-mg=ma,\)
\(\displaystyle 2mg-F=(2m)(2a).\)
Az egyenletrendszer megoldása: \(\displaystyle a=\tfrac13 g\) és \(\displaystyle F=\tfrac23 mg\).
Az \(\displaystyle m\) tömegű test tehát \(\displaystyle a_1=\tfrac13 g\) gyorsulással indul el felfelé, a \(\displaystyle 2m\) tömegű test pedig \(\displaystyle a_2=\tfrac23 g\) gyorsulással indul el lefelé.
Statisztika:
58 dolgozat érkezett. 4 pontot kapott: Balaskó Dominik, Bartók Imre, Boros Máté, Bukor Benedek, Conrád Márk, Csuha Boglárka, Fekete Balázs Attila, Guba Zoltán, Hajdu 046 Ákos, Kavas Katalin, Kolontári Péter, Kozák András, Krasznai Anna, Magyar Róbert Attila, Marozsák Tóbiás , Molnár Mátyás, Morvai Orsolya, Olosz Adél, Ónodi Gergely, Paulovics Péter, Póta Balázs, Richlik Róbert, Sal Dávid, Tófalusi Ádám, Varga-Umbrich Eszter, Weisz Máté, Zöllner András. 3 pontot kapott: Berke Martin, Édes Lili, Keltai Dóra, Klučka Vivien, Makovsky Mihály, Mamuzsics Gergő Bence, Markó Gábor, Nagy 555 Botond, Németh 123 Balázs, Németh Csaba Tibor, Páhoki Tamás, Schrott Márton. 2 pontot kapott: 9 versenyző. 1 pontot kapott: 9 versenyző. 0 pontot kapott: 1 versenyző.
A KöMaL 2017. áprilisi fizika feladatai

