 Problem P. 4941. (May 2017)
Problem P. 4941. (May 2017)
P. 4941. In a big water reservoir the height of the water is \(\displaystyle H\). Next to the reservoir there are \(\displaystyle N\) number of cylinder shaped water tanks (each at the level of the bottom of the reservoir). The tanks are connected with alike thin tubes. The water tank at one end of the tank system is connected to the bottom of the reservoir through a thicker tube, whilst at the other end of the tank system there is an – initially closed – tap.
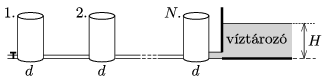
If the tap is opened, then after a long enough time the total volume of the water in the tanks decreases by a value of \(\displaystyle V_0\). What is the diameter of the tanks? (The flow of the water is viscous.)
(4 pont)
Deadline expired on June 12, 2017.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Kezdetben mindegyik tartályban \(\displaystyle H\) magasságú a víz (közlekedőedény elve). Ha kinyitjuk a csapot, a legutolsó tartály gyakorlatilag teljesen kiürül, a legelsőben – jó közelítéssel – marad a \(\displaystyle H\) magasság. A közbenső tartályokban számtani sorozat szerint változik a vízmagasság, hiszen az egyforma hosszú csövekben (az egyensúlyi áramlási állapot beállta után) ugyanannyit esik a nyomás. A vízmagasságok tehát:
\(\displaystyle 0, \quad \frac{1}{N-1}H, \quad \frac{2}{N-1}H,\ldots , \frac{N-1}{N-1}H,\)
a tartályokban lévő víz térfogata pedig:
\(\displaystyle NH\frac{d^2\pi}{4}-V_0=\frac{d^2\pi}{4}\frac{H}{(N-1)}\,(1+2+\ldots +(N-1)), \)
ahonnan
\(\displaystyle d=\sqrt{\frac{8V_0}{H\pi N}}.\)
Statistics:
9 students sent a solution. 4 points: Bukor Benedek, Fekete Balázs Attila, Kolontári Péter, Mamuzsics Gergő Bence, Molnár Mátyás, Morvai Orsolya, Páhoki Tamás, Tófalusi Ádám. 3 points: Pszota Máté.
Problems in Physics of KöMaL, May 2017
