Problem P. 4946. (May 2017)

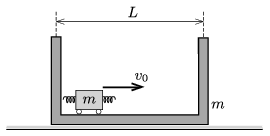
P. 4946. A trolley of mass \(\displaystyle m\) can move freely in a box of mass \(\displaystyle m\). The box can move on the tabletop which is covered by a thin layer of oil, the frictional force depends on only the speed of the box: \(\displaystyle \boldsymbol F=-k\boldsymbol v\). Initially the box stays at rest, and the trolley starts from the wall on the left-hand side at a speed of \(\displaystyle v_0\) and moves towards the wall on the right. How many times will the trolley of length \(\displaystyle \ell\) collide elastically with the box of length \(\displaystyle L\)? (The elastic collision is ensured by the small springs attached to the trolley, their length is much smaller than \(\displaystyle \ell\).)

(5 pont)

Deadline expired on June 12, 2017.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. A kiskocsi jobb oldalon ütközik a dobozzal, ekkor ,,sebességet cserélnek''. A doboz lassulva mozog, megtesz \(\displaystyle L-\ell\) utat (ha közben meg nem áll), és a bal oldalánál ütközik a kiskocsival. Ekkor a doboz megáll, és a kiskocsi valamekkora \(\displaystyle v_1<v_0\) sebességgel elindul jobbra. Ez ismétlődik egészen a doboz megállásáig.

A doboz mozgása szempontjából érdektelenek azok az időtartamok, amikor a doboz áll és csak a kiskocsi mozog, ezeket tehát el is hagyhatjuk, és úgy tekinthetjük, mintha a doboz folyamatosan mozgott volna az

\(\displaystyle F= \frac{\Delta(mv)}{\Delta t}=-kv=-k\frac{\Delta x}{\Delta t} \)

mozgásegyenlet szerint. Ebből leolvasható, hogy \(\displaystyle \Delta(mv(t)+kx(t))=0,\) vagyis az \(\displaystyle mv(t)+kx(t)\) mennyiség időben állandó. Mivel kezdetben \(\displaystyle v=v_0\), látható, hogy a doboz összesen \(\displaystyle s=mv_0/k\) utat tesz meg a megállásáig. (Az ehhez szükséges idő ,,végtelen'' hosszú, mert a sebessége exponenciálisan csökken nullára.) Az ütközések száma

\(\displaystyle N=2\left[\frac{s}{L-\ell} \right] +1,\)

ahol \(\displaystyle [x]\) az egészrész-függvényt (\(\displaystyle x\)-nél nem nagyobb egész számot) jelöli.

Statistics:

24 students sent a solution.
5 points:	Bekes Nándor, Elek Péter, Fajszi Bulcsú, Fehér 169 Szilveszter, Fekete Balázs Attila, Illés Gergely, Kondákor Márk, Kozák András, Krasznai Anna, Marozsák Tóbiás , Nagy 555 Botond, Németh 123 Balázs, Németh 777 Róbert, Olosz Adél, Ónodi Gergely, Osváth Botond, Páhoki Tamás, Szentivánszki Soma , Tófalusi Ádám, Weisz Máté.
4 points:	Jakus Balázs István, Sal Dávid.
3 points:	1 student.
2 points:	1 student.

Problems in Physics of KöMaL, May 2017