 Problem S. 15. (February 2006)
Problem S. 15. (February 2006)
S. 15. Write a program that solves Sam Lloyd's famous puzzle of arranging numbered tiles in a 3×3 square. We have 8 tiles in a 3×3 box, so there is one empty position. The tiles are numbered from 1 to 8. In one step one moves an adjacent tile to the empty position. Our aim is to have numbers 1, 2, 3 in the first row, 4, 5, 6 in the second, while 7, 8 and the empty position in the third row.
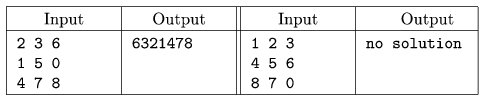
Your program should read the initial state from the standard input. This will consist of 3 lines, with 3 numbers in each line separated by spaces. A 0 indicates the empty position.
Your program should find the shortest solution (that is, the one consisting of the least number of steps) and print it to the standard output. If there are more than one shortest solutions, any of them can be chosen to be displayed. One step is represented as the number of tile being moved. Numbers should be displayed in one line, without spaces. If there is no solution, simply display ,,no solution''.
Examples:
The source code of the program (s15.pas, s15.cpp, ...) should be submitted.
(10 pont)
Deadline expired on March 16, 2006.
Statistics:
4 students sent a solution. 10 points: Engedy Balázs, Nikházy László. 9 points: Ureczky Bálint. 3 points: 1 student.
Problems in Information Technology of KöMaL, February 2006
