Problem S. 16. (March 2006)

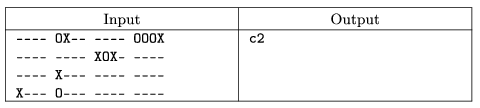
S. 16. Write a program to suggest a step in the ``3D Tic-Tac-Toe'' game in an arbitrary position. It is a game for two players. The board consists of 4×4 vertical sticks. Players place a token (pierced balls) onto the sticks in turn. The first player has light tokens, the other one has dark. Every stick can hold 4 tokens, so that there are 4³=64 tokens altogether. The player who is first to set four tokens in a straight line, either horizontally, vertically or diagonally, has won. Otherwise, if all 64 tokens are set without a straight line, the game is a draw (see the figure).

The sticks are labelled as the squares on the chessboard by a1, ..., d4.

Your program reads the standard input to get the initial state of the board. Each row contains the content of 4 sticks. Tokens of the computer are denoted by O, while tokens of the opponent are denoted by X. An empty space is denoted by a -. The first row contains sticks a1, a2, a3, a4, the second row contains sticks b1, ..., b4, and so on.

Your program should write the name of the recommended stick as the next step to the standard output.

Solutions will be tested on a 2 GHz machine, the answer in a situation should be given within 10 seconds. We will make a tournament among the submitted programs, the winner receives 10 points, the second one 8, while the others get at most 7 points -- provided they come with an adequate documentation.

See the example.

The source code of the program (s16.pas, s16.cpp, ...) and its documentation is to be submitted. (10 points)

(10 pont)

Deadline expired on April 18, 2006.

Statistics:

6 students sent a solution.
9 points:	Engedy Balázs.
8 points:	1 student.
7 points:	1 student.
6 points:	2 students.
3 points:	1 student.

Problems in Information Technology of KöMaL, March 2006