Problem S. 42. (February 2009)

S. 42. Create a program capable of playing the following variant of ``Tetris''.

The playing field is a grid consisting of unit squares. The left, right and bottom sides of the playing area are closed walls, only the upper part is open. Various shapes composed of unit squares fall down the playing field randomly, one by one, from infinite height, and the player has to stack these shapes. The aim is to properly position these shapes such that the height of this continuously growing tower is minimal.

A shape is properly positioned on the playing field, if

- it is disjoint from any other shapes, and if

- the bottom of at least one of its unit square components touches a previously positioned shape, or touches the bottom wall of the playing field, and if

- it is possible to position the shape as a composition of a rotation and horizontal translation (performed infinitely high above the bottom wall), then a vertical dropping, such that the current shape does not overlap with any other shapes already on the playing field during this operation.

Possible shapes are encoded by 6 letters (see the Figure).

During execution, your program interactively communicates with a main application via the standard input and output, by using newline-separated text messages. The main application is responsible for producing the next random shape and checking the answers. If an event happens, the main application notifies your program by sending a message on the standard input in the following syntax:

start <W>

o It is sent only once, at the beginning of the game, and gives the width of the playing area 3W32. This message should not be answered by your program.

item [ojlszi]

o A new shape encoded by one of the six letters o, j, l, s, z or i will arrive next. The answer by your program to this should be a pos message.

Your program should write only the following type of message on the standard output in the following syntax:

pos <position of the left side of the shape after rotation> <rotation\ anticlockwise in degrees>

o This is the expected answer to an item message. It describes the requested position of the actual shape: in which row to position its left side after the rotation (an integer between 1 and W-s+1, with s being the width of the shape after rotation), further, the angle of the rotation (being 0, 90, 180 or 270 degrees anticlockwise).

Your program gets a message from the standard input describing the next shape only after the position of the previous item has been written on the standard output. Always use the standard input and output (and not the keyboard or the screen). Always put a newline-character at the end of each message and clear the output buffer after the message has been sent. In case of Pascal, do not use the Crt module, and in case of C or C++, conio.h is not allowed.

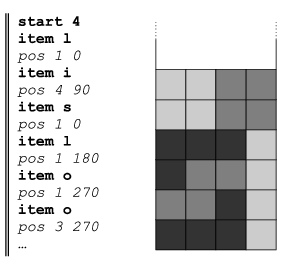
The example (see the figure) contains a possible dialogue between your program and the main application (the answers of your program are in italics).

(10 pont)

Deadline expired on March 16, 2009.

Sorry, the solution is available only in Hungarian. Google translation

A megoldás menete

Nyilvánvaló, hogy mivel az n-edik elemet az előtt kell elhelyeznünk, hogy bármiféle információval rendelkeznénk az n+1-edik és további elemekről, illetve a játék akármelyik pillanatban abbamaradhat, a problémára tökéletes megoldás nem adható. A feladat egy minél jobb közelítő (heurisztikus) megoldás elkészítése volt, két szempontból is: egyrészt egy olyan megoldást kellett adni, mely olyan tornyot épített, melynek magasságát bármikor mintavételezve átlagosan minél kisebb értéket kapunk (tehát nem feltétlen minden pillanatban optimális, de mindig közel van az optimumhoz), másrészt a gyorsaság érdekében az elemek elhelyezését célszerű volt valamilyen jóságfüggvény alapján végezni, ahelyett, hogy fabejárással a döntés lehetséges következményeit vizsgálnánk az összes lehetséges következő N elem esetén.

Egy új elem adott elhelyezésének értékelése során két szempontot volt célszerű figyelembe venni: egyrészt azt, hogy a torony magassága a lehető legkisebb mértékben növekedjen, másrészt pedig, hogy a lehető legkevesebb "lyuk" (azaz elem alatti üres hely) keletkezzen. Önmagában egyik módszer sem vezetett túl jó eredményre: amennyiben valaki csak a magasság rövid távú minimalizálására törekedett, úgy általában túl sok lyukat hozott létre, mely a magasságot hosszú távon jelentősen hátrányosan befolyásolta. Ha a lyukak minimalizálása volt az elsődleges (és azonos lyukszám esetén nyilvánvalóan jobbnak kell választani a kisebb magasságút), az - szerencsétlen elemsorozat esetén - általában ahhoz vezetett, hogy a torony tetején nyúlványok kezdtek el képződni: pl. ha nem jött olyan elem, amivel a torony közepét és széleit lehetett volna lyukmentesen lefedni, akkor gyakran a torony egyharmadánál és kétharmadánál kisebb tornyok kezdtek el épülni. Szerencsés esetben egy idő után a megfelelő elemek érkezésével ezek a völgyek feltöltődtek, de nem ritkán előfordult az is, hogy a megoldás kényszerhelyzetbe került, és nem tudott mást tenni, mint úgy elhelyezni egy elemet, hogy az rálógott egy ilyen völgy nyílására: katasztrofális következmény.

A legjobb heurisztika úgy adódik, hogy amennyiben nem okoz (a torony felszínén) túl nagy magasságkülönbséget a lyukmentes elhelyezés, azt választjuk, egyébként pedig feláldozunk néhány lyukat a nyúlványok elkerülése érdekében. További (megfelelő elemhalmaz esetén minimális) javulás érhető el, ha az elemek elhelyezésekor figyelünk arra, hogy a fenti megfontolásokon túl úgy helyezzük azokat el, hogy a későbbiekben minél jobban tudjunk rájuk építkezni.

Ezek után már csak ki kellett értékelni a lehetséges elhelyezéseket, és a legjobb elhelyezést kiválasztani. Ez legfeljebb W-vel arányos lépés, ha pályáról csak azt tároljuk, hogy az adott oszlopban milyen magasan helyezkedik el a legfelső elem -- vegyük észre, hogy ennyi elegendő is.

A beérkezett megoldások értékelése

A feladatra sok kiváló megoldás érkezett, melyeknek nagyon örültünk.

A pontozás a következőképpen alakult: a programra, attól függően, hogy a megoldás mennyire volt optimális, legfeljebb 8 pontot lehetett kapni, a megfelelő dokumentáció és az olvasható, jól kommentezett kód 2 pontot ért. A működőképes (és az azzá tett) megoldások között versenyt szerveztünk, mely során I., II. és III. díjat osztottunk ki. Az első díjért legfeljebb 8, másodikért 7, a harmadik díjért pedig legfeljebb 6 pontot lehetett kapni, a nem díjazott megoldások a "program" részre legfeljebb 5 pontot kaphattak. Amennyiben a program versenyképes állapotba juttatásához azon javítás(oka)t kellett végezni, az elért eredményre kapott pontszámot a hibá(k) súlyosságának megfelelően csökkentettük. Szeretnénk hangsúlyozni, hogy az igazságos pontozás érdekében a programokban kizárólag olyan hibákat javítottunk, melyek hatására a program belső pályareprezentációja sérült, vagy a javítókörnyezet számára küldött "pos" üzenetet nem azt az elemelhelyezést írta le, melyre a program gondolt: ezek a hibák ugyanis inkonzisztenciát eredményeztek a pálya tényleges állapota, illetve a között az állapot között, amelyben az adott program a pályát elképzelte, és hosszú távon teljesen rossz elemelhelyzésekhez vezettek (hiszen a program és a javítókörnyezet nem ugyanazon a pályán dolgozott). Ezek pedig értékelhetetlen eredményekhez vezettek, de legalább ugyanebből az okból kifolyólag ezen hibák jól detektálhatóak is voltak, így ezeket nagy biztonsággal javítani tudtuk. Az elemek szuboptimális elhelyezését eredményező implementációs hibák javítására viszont nem vállalkoztunk, ugyanis ezek egyrészt rendkívül nehezen azonosíthatóak, másrészt nehezen eldönthető, hogy egy adott programsor implementációs vagy elvi hibát tartalmaz, harmadrészt pedig egy sor javításával a megoldás teljesítménye (jósága) lényegesen megváltozhat, melynek következtében szinte lehetetlen lett volna ezen javításokat is figyelembe vevő, igazságos pontrendszert kidolgozni.

A versenyzők megoldásainak egy-egy 4, 8, 12, 16, 20, 24, 28, ill. 32 széles pályán kellett rendre 1000 elemet elhelyezni. A javítókörnyezet végezte az elemek sorsolását, elhelyezéseinek ellenőrzését, a lépések aktualizálását, majd rögzítését, illetve statisztikát is vezetett. A 17 beérkezett megoldás közül 13 vett részt az egymás elleni küzdelemben. Az egyes megoldások által épített tornyok magassága a különféle szélességű pályákon az 1000. elem elhelyezése után rendre a következő: (a -1 azt jelenti, hogy a program szabálytalan lépést tett)

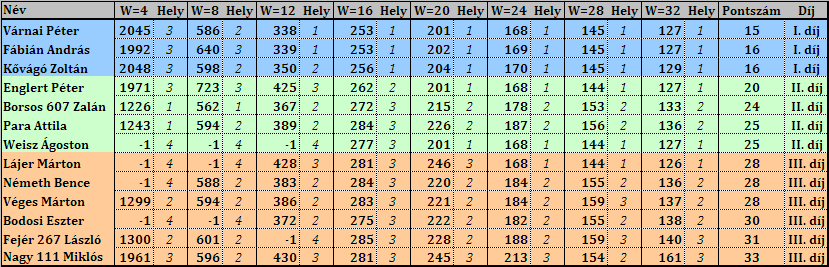
A különböző méretű pályákon az egyes megoldásokat rangsoroltuk: a legjobb megoldások 1 pontot, a közepesen teljesítők 2-t, a gyengébben teljesítők 3-at, az illegális lépést végrehajtók 4 pontot kaptak. Az így kapott pontokat minden megoldásra összegeztük, és az így kapott pontszámokból alakítottuk ki a fenti rangsort. (A legkisebb 3 és a legnagyobb pálya csak félpontot ért.)

Részletes statisztikák

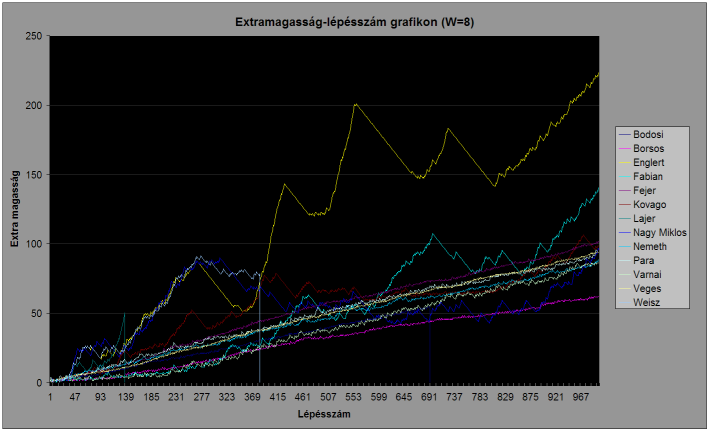
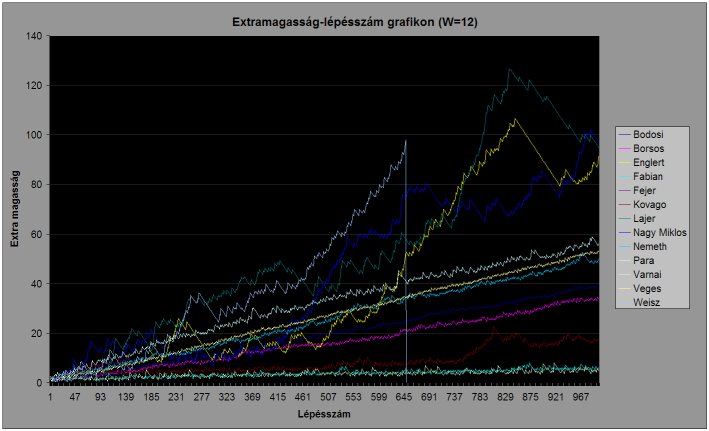
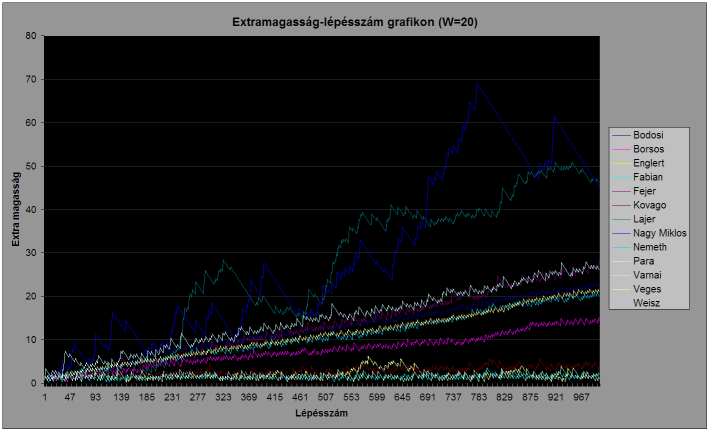
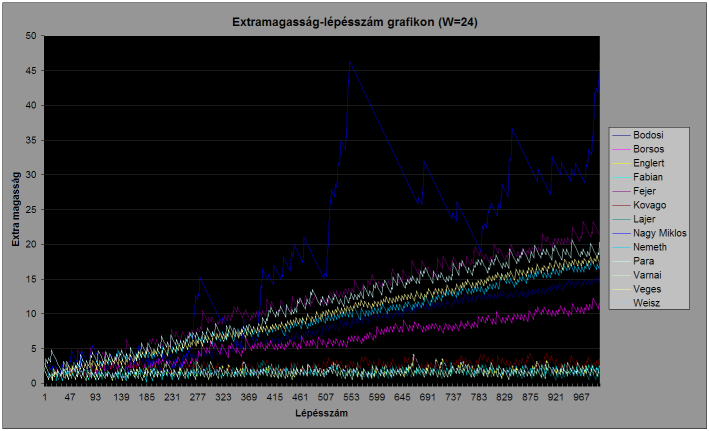
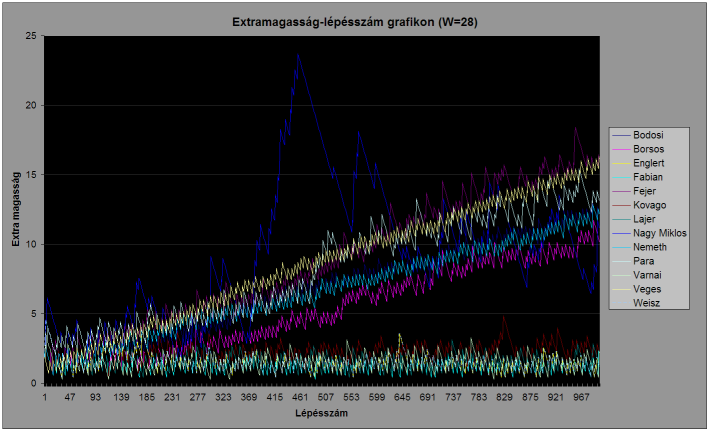
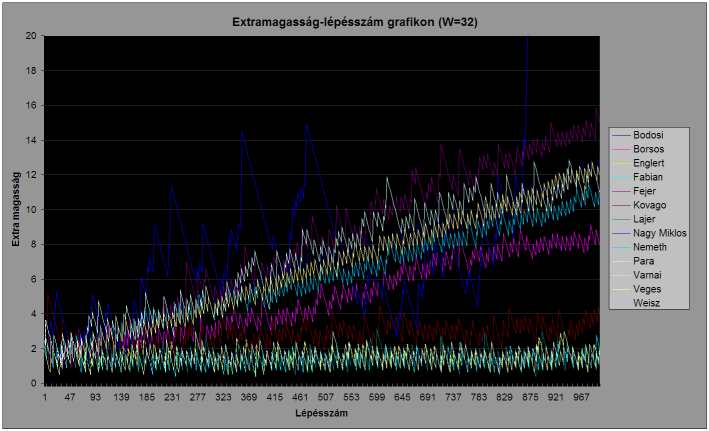
Az egyes pályákon a versenyzők által épített tornyok magasságának és az optimális torony magasságának a különbsége (aka.: extra magasság) a lépésszám függvényében:

A részletes teszteredmények, az építményekről készült képekkel innen letölthetőek (vigyázat, 10MB!).

Gyakori hibák

A legtöbb versenyzőnél előfordult, hogy a kimenetre írás után a kimeneti puffert nem ürítették (flush vagy annak megfelelő utasítással), melynek hatására a válasz "elakadt" a standard kimeneti csővezeték pufferében, így azt a javítókörnyezet nem tudta kiolvasni.

Néhány versenyzőnek a feladat pontos értelmezésével akadt problémája, ilyen esetekben bátran kérdezzetek a fórumon!

Mintamegoldás

Mintamegoldásként közöljük:

- Fábián András, 12. osztály, Szeged, Radnóti Miklós Kísérleti Gimnázium (Pascal, fabian.zip)

- Kovágó Zoltán, 9. osztály, Budapest, Szent István Gimnázium (C++, kovago.zip)

- Várnai Péter, 10. osztály, Budapest, ELTE Apáczai Csere János Gyakorló Gimnázium (FreeBASIC, varnai.zip)

versenyzők munkáját.

Statistics:

17 students sent a solution.
10 points:	Fábián András, Kővágó Zoltán, Várnai Péter.
9 points:	Englert Péter, Weisz Ágoston.
8 points:	4 students.
7 points:	3 students.
6 points:	1 student.
5 points:	1 student.
4 points:	1 student.
3 points:	1 student.
1 point:	1 student.

Problems in Information Technology of KöMaL, February 2009