 Problem S. 44. (April 2009)
Problem S. 44. (April 2009)
S. 44. A tram competition is organized on the longest tram line of the city. The goal is to travel the whole line in the shortest possible time, but at the same time there should be only one competitor on the line. During the contest trams do not carry passengers, but the organizers do not want to restrict car traffic in the city, so there is a second rule for competitors saying that a tram must stop if they encounter a red traffic lamp at a crossing.
Your program should compute the minimal time to travel the whole line. The input file (as the first command line argument to your program) contains the description of the tram line, while your result should be written in the output file (with name given as the second command line argument).
The front of the tram is located at x=0 in the coordinate system at time t=0. At the beginning of each time unit, the tram can change its speed instantaneously by -1, 0 or +1 unit. Then the tram travels uniformly at this speed for one time unit along the x-axis. The tram can stop but can not travel in the reverse direction. Its maximal speed is limited by a given constant M.
The front part of the tram can pass through a crossing only if the lamp shows green. State of the lamps are described by left-open and right-closed intervals, meaning that a tram can still cross if the lamp has just turned red, but the tram should not cross if the lamp has just turned green. A tram has completed the line if the x-coordinate of its front is equal to the length L of the line.
The first three rows of the input file contain three numbers separated by a space: the length 10 L
L 5000 of the line, the number 0
5000 of the line, the number 0 N
N 1000 of traffic lamps and the maximal allowed speed 1
1000 of traffic lamps and the maximal allowed speed 1 M
M 30 of the tram. Then each of the following N lines contains the description of the actual lamp: the position 1
30 of the tram. Then each of the following N lines contains the description of the actual lamp: the position 1 Xi
Xi L of the lamp, the number 1
L of the lamp, the number 1 Ci
Ci 100 of changing its state (but altogether at most 1000 changes), then Ci numbers, separated by a space, describing the time instants
100 of changing its state (but altogether at most 1000 changes), then Ci numbers, separated by a space, describing the time instants when the lamp changes between red and green. Initially, all lamps show green.
The output should contain only one number: the shortest time in which a tram can travel through the line. The number should be given in integer part-fractional part form, , where c is the speed of the tram at the last instant.
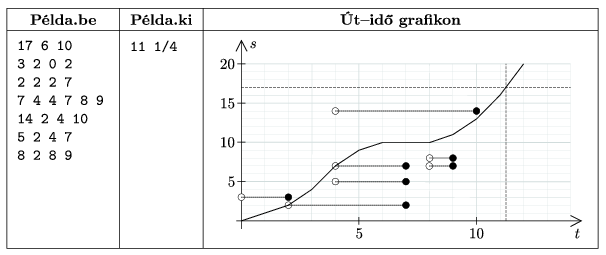
In the example, ``Példa.be'' is the name of the sample input file, ``Példa.ki'' is the output file, and ``Út-idő grafikon'' is ``path--time diagram''.
In order to get maximal points, the running time of your program should be within a few minutes on a modern PC even for larger data sets. The task can be solved in 64 kB of memory, and the above time limit also refers to such solutions, so we do not recommend using temporary files in any cases.
The source code of your program (s44.pas, s44.cpp, ...) and a short documentation (s44.txt, s44.pdf, ...) should be submitted, also describing your solution and specifying the name of the developer environment to use for compiling, further, the possible parameters of your program.
Clarification: In case the tram comes to a halt at a crossing, it is considered "passing through" that respective crossing momentarily so long as it stands still (including the moment it stopped and will start).
(10 pont)
Deadline expired on May 15, 2009.
Sorry, the solution is available only in Hungarian. Google translation
A megoldás menete
A feladat megoldásához célszerű volt bevetni a dinamikus programozás módszerét. A módszert olyan optimalizációs feladatok esetén célszerű alkalmazni, ahol a teljes probléma optimális megoldása felírható valamilyen részproblémák megoldásainak ismeretében, illetve egy-egy részmegoldásra többször is szükség van.
Formalizáljuk tehát a feladatot a következőképp. Legyen P[t,x,v] az ún. elérhetőségi mátrix: egy olyan háromdimenziós, logikai értékekből álló táblázat, melynek (t,x,v) eleme akkor és csak akkor igaz, ha a villamos a t időpillantban érkezhet v sebességgel az x koordinátájú pontba. A feladat ennek a mátrixnak a kitöltése. Ha ez megvan (elegendő t időig), akkor mindössze annyit kell tennünk az eredeti feladat megoldásához, hogy megvizsgáljuk, hogy melyik legkisebb t1 értéknél van először x L pozícióhoz tartozó cellában igaz érték. Ha több ilyen is van, akkor azt kiválasztjuk, amelyhez tartozó út a legkorábban metszi az x=L egyenest.
L pozícióhoz tartozó cellában igaz érték. Ha több ilyen is van, akkor azt kiválasztjuk, amelyhez tartozó út a legkorábban metszi az x=L egyenest.
De hogyan töltsük ki a táblázatot? A t=0-hoz tartozó cellák kitöltése egyszerű: P[0,0,0]=igaz, minden más x és v-re P[0,x,v]=hamis, hiszen tudjuk, hogy t=0-ban a villamos az origóban áll. Definiáljunk továbbá egy L[t,x] függvényt, mely igaz, ha a t időben az x helyen a lámpa piros. A további értékek kitöltése így magától értetődik:
feltéve, hogy az értelmezési tartományon kívül koordinátákra P[t,x,v]=0. Érdemes megfigyelni, hogy a t+1. időszelet kitöltéséhez elegendő csupán a t. időszelet értékeit ismerni: tehát nem szükséges az egész mátrixot eltárolni, elegendő csupán 2 szeletét... vagy akár 1 szeletét, ha megoldjuk, hogy ne írják felül egymást az értékek (pl. jó sorrendben frissítjük).
A megoldások értékelése
A megoldások nagy része backtracking módszerrel kísérelte meg a feladatot megoldani, azonban ezek a megoldások a megfelelő korlátozó feltételek híján már a közepes méretű bemenetekre sem futottak le időben. Volt azonban néhány dinamikus programozást használó megoldás is, melyeknek nagyon örültünk.
Rendkívül sok megoldás esetén találkoztunk implementációs hibákkal -- gyakran olyan súlyosakkal, melyek hatására majd' az összes tesztbemenetre hibás eredmény született. A hibák általában elírásból, elnézésből fakadnak, ezért nem győzzük hangsúlyozni annak fontosságát, hogy a programokat beadás előtt magatok is teszteljétek!
Mintamegoldás, tesztesetek, szemléltetőprogram
Pascal mintamegoldás, Englert Péter, 12. osztályos versenyző (Zrínyi Miklós Gimnázium, Zalaegerszeg) munkája alapján: englert.zip
Hivatalos mintamegoldás C++ nyekven: mmo.cpp
Tesztesetek: javit.zip
Interaktív szemléltetőprogram: TestGenerator.zip
Statistics:
13 students sent a solution. 10 points: Véges Márton. 8 points: 2 students. 7 points: 2 students. 6 points: 2 students. 5 points: 4 students. 4 points: 2 students.
Problems in Information Technology of KöMaL, April 2009
